-
Решается легко довольно, но у меня не получается. Кто решит, тому отдам все 40 баллов, если количество баллов Вас интересует, ну или вы просто добрая душа со светлой душой, которая помогает всем и вся.
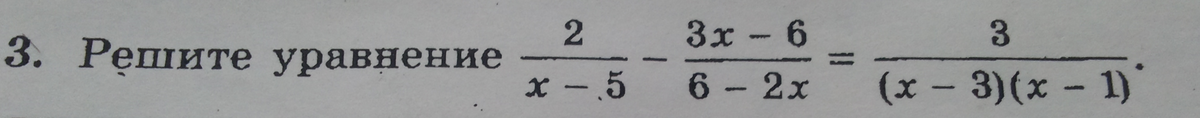
Ответы 3
-
не так уж и легко
-
Автор:
jacobsalazar - 6 лет назад
-
0
-
-
спасибо, солнышко)
-
Автор:
allieemml - 6 лет назад
-
0
-
-
Представим 3/(х-3)(х-1) в виде суммы дробей3/(x-3)(x-1)=A/(x-3)+B/(x-1)=(Ax-A+Bx-3B)/(x-3)(x-1)==[x(A+B)+(-A-3B)]/(x-3)(x-1)A+B=0⇒A=-B-A-3B=3B-3B=3-2B=3B=-3/2A=3/23/(x-3)(x-1)=3/2(x-3)-3/2(x-1)подставим в уравнение2/(x-5)+(3x-6)/2(x-3)=3/2(x-3)-3/2(x-1)2/(x-5)+(3x-6)/2(x-3)-3/2(x-3)+3/2(x-1)=02/(x-5)+(3x-6-3)/2(x-3)+3/2(x-1)=02/(x-5)+(3x-9)/2(x-3)+3/2(x-1)=02/(x-5)+3(x-3)/2(x-3)+3/2(x-1)=02/(x-5)+3/2+3/(2(x-1)=0x≠5;x≠14(x-1)+3(x-5)(x-1)+3(x-5)=04x-4+3x²-18x+15+3x-15=03x²-11x-4=0D=121+48=169x1=(11-13)/6=-1/3x2=(11+13)/6=4
-
Автор:
spicylfzo - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
помогите с примером
1 разделить на дробь 12/210-
Предмет:
Математика -
Автор:
lucapowers - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
достопримечательности росии и чем они славятся
-
Предмет:
История -
Автор:
gerardokeller - 6 лет назад
-
Ответов:
3 -
Смотреть
-
- На склад привезли 100 кг огурцов, влажность которых равна 99%.за время хранения влажность огурцов уменьшилась на 1%.сколько стали весить огурцы
-
какой суффикс в слове покраснел
-
Предмет:
Русский язык -
Автор:
beansvgqh - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
