-
Сделать задание . Оно есть в файле. Для функции f(x) найти первоначальную, график которой проходит через такие точки как M (1;5).
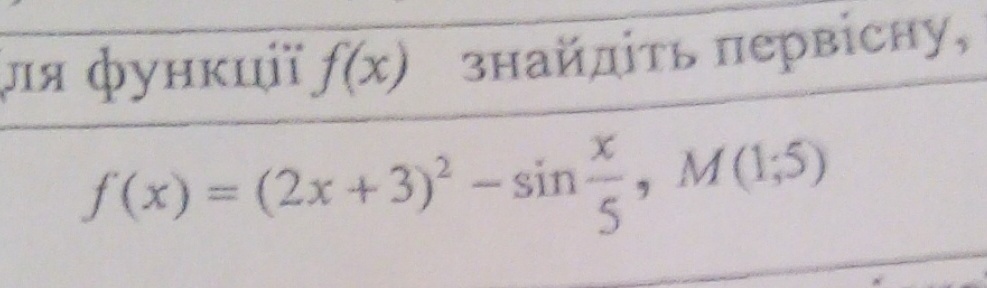
-
Предмет:
Алгебра -
Автор:
joecabrera - 5 лет назад
-
Ответы 2
-
F(x)=1/6*(2x+3)³+5cosx/5+C1/6*125+5cos1/5+C=5C=5-125/6-5cos0,2=-15 5/6-5cos0,2F(x)=1/6*(2x+3)³+5cosx/5-15 5/6-5cos0,2
-
Автор:
ronnie - 5 лет назад
-
0
-
-
Найдем неопределенный интеграл данной функции:
Откуда:
Теперь найдем первообразную для точки M. Для этого нам нужно значение икса в данной точке и значение функции в данной точке. После этого мы узнаем константу C, которая нам и нужна для описания первообразной проходящей через точку М:
Отсюда и первообразная:
-
Автор:
baxter - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Слово атмосфера многозначное или омоним?
-
Предмет:
Русский язык -
Автор:
sparkle84n2 - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Помогите пожалуйста с задачей.
Два автомобиля одинаковой массы 1000 кг движутся со скоростями 10 м/с и 20 м/с относительно Земли в противоположных направлениях. Чему равен модуль импульса второго автомобиля в системе отсчета, связанной с первым автомобилем? -
В тундре покрытой десять месяцев снегом своеобразно растительность.Изумительны эти необыкновенные растения оживающие под снегом. Их стебли и листья покрыты тёплым и густым пухом спасающим от стужи.Многие растения образующие круглые цветнечки плотно жмутся друг к дружке. В их корнях обросших пушистой шубкой прячутся насекомые, устраивают гнезда лемминги и полёвки. Только у немногих северных растений цветущих весной созревают за лето семена. Большинство растений сохранившихся от доледниковых времен продолжают размножаться вегетативно.
Задание:
1)Выписать словосочетание со сострадательными причастиями
2)выпишите словосочетания с действительными причастиями
3)выпишите краткие причастия
4)Расставьте в тексте знаки препинания.-
Предмет:
Русский язык -
Автор:
kylee - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Найдите в предложениях нарушения литературных норм, напишите исправленный вариант
1. «Известия» напечатала репортаж с места событий.
2. Участковая врач работала в поликлинике десять лет, но недавно она
перешла на другую работу.-
Предмет:
Русский язык -
Автор:
puffyclements - 5 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
