Высота основания правильной треугольной пирамиды равна 2 см, боковое ребро составляет с высотой пирамиды угол 30 градусов. Найти V

Ответ:

Объем пирамиды равен \displaystyle 1\frac{7}{9}  см³.

Объяснение:

Высота основания правильной треугольной пирамиды равна 2 см, боковое ребро составляет с высотой пирамиды угол 30 градусов. Найти V.

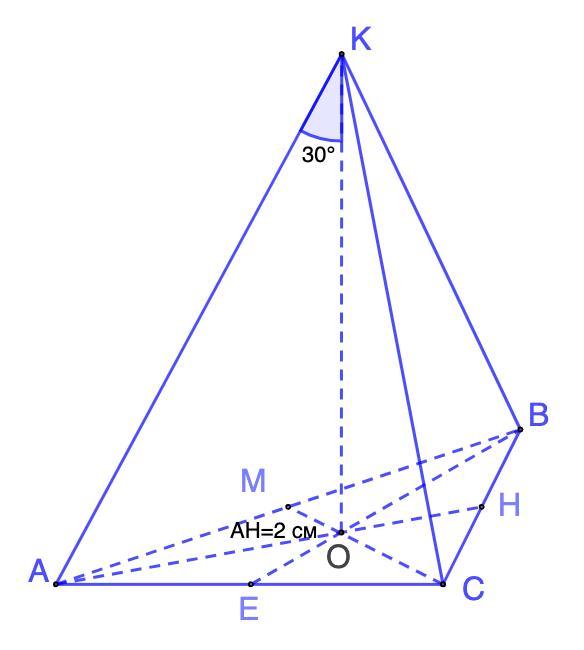
Дано: КАВС - правильная пирамида;

АН = 2 см - высота основания;

∠АКО = 30°.

Найти: V(КАВС)

Решение:

• Объем пирамиды найдем по формуле:

где Sосн. - площадь основания, h - высота пирамиды.

Найдем площадь основания.

• В основании правильной треугольной пирамиды лежит равносторонний треугольник.

⇒ ΔАВС - равносторонний.

• Площадь равностороннего треугольника равна:

где а - сторона треугольника.

• Углы равностороннего треугольника равны 60°.

• Синус угла - отношение противолежащего катета к гипотенузе.

\displaystyle sin\;60^0=\frac{AH}{AC} \\\\\frac{\sqrt{3} }{2}=\frac{2}{AC}\\ \\ AC=\frac{4}{\sqrt{3} }\;_{(CM)}

Площадь основания равна:

\displaystyle S(ABC)=\frac{\sqrt{3}\cdot 16 }{4\cdot 3}=\frac{4\sqrt{3} }{3} \;_{(CM^2)}

• Вершина правильной пирамиды проецируется на основание в точку пересечения медиан (высот, биссектрис).

• Медианы пересекаются в одной точке и делятся точкой пересечения в отношении 2 : 1, считая от вершины.

⇒ АО - 2 части, ОН - 1 часть.

Тогда

\displaystyle AO=\frac{AH\cdot2}{3} =\frac{2 \cdot2}{3} =\frac{4}{3} \;_{(CM)}

Найдем высоту пирамиды.

Рассмотрим ΔАКО - прямоугольный.

• Тангенс угла - отношение противолежащего катета к прилежащему.

\displaystyle tg\;30^0 = \frac{AO}{KO} \\\\\frac{\sqrt{3} }{3}=\frac{4}{3\cdot KO} \\\\KO=\frac{3\cdot 4}{\sqrt{3}\cdot 3 } =\frac{4}{\sqrt{3} }\;_{(CM)

Найдем объем пирамиды:

\displaystyle V(KABC)=\frac{1}{3}\cdot \frac{4\sqrt{3} }{3}\cdot \frac{4 }{\sqrt{3} } =\frac{16}{9}=1\frac{7}{9} \;_{(CM^3)}

Объем пирамиды равен \displaystyle 1\frac{7}{9}  см³.

#SPJ1