-
Я гуманитарий)Очень нужна помощь. Помогите решить уравнения и неравенства. Заранее спасибо.
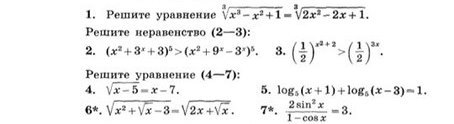
Ответы 1
-
1Возведем в куб обе части уравненияx³-x²+1=2x²-2x+1x³-x²+1-2x²+2x-1=0x³-3x²+2x=0x(x²-3x+2)=0x=0x²-3x+2=0x1+x2=3 U x1*x2=2x=1 U x=2Ответ x={0;1;2}2Степени одинаковые,сравним основанияx²+3^x+3>x²+9^x-3^xx²+9^x-3^x-x²-3^x-3<09^x-2*3^x-3<0a=3^xa²-2a-3<0a1+a2=2 U a1*a2=-3a1=-1 U a2=3-1<a<3⇒-1<3^x<3⇒x<1x∈(-∞;1)3Основание меньше 1,значит знак неравенства изменитсяx²+2<3xx²-3x+2<0x1+x2=3 u x1*x2=2x1=1 u x2=2x∈(1;2)4ОДзx-5≥0⇒x≥5x-7≥0⇒x≥7x∈[7;∞)Возведем в квадрат обе части уравненияx-5=x²-14x+49x²-15x+54=0x1+x2=15 U x1*x2=54x1=6x2=95ОДЗx+1>0⇒x>-1x-3>0⇒x>3log(5)[(x+1)(x-3)]=1(x+1)(x-3)=5x²-3x+x-3-5=0x²-2x-8=0x1+x2=2 U x1*x2=-8x1=-2 не удов услx2=46x>0Возведем в квадрат обе части уравненияx²+√x-3=2x+√xx²+√x-3-2x-√x=0x²-2x-3=0x1+x2=2 U x1*x2=-3x1=-1 не удов услx2=371-cosx≠0⇒cosx≠1⇒x≠2πn,n∈z2sin²x=3-3cosx3-3cosx-2+2cos²x=0cosx=a2a²-3a+1=0D=9-8=1a1=(3-1)/4=1/2⇒cosx=1/2⇒x=+-π/3+2πk,k∈za2=(3+1)/4=1⇒cosx=1 не удов усл
-
Автор:
alinatagg - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Известно, что зрительная зона коры больших полушарий находится в затылочной доле. Будет ли видеть человек, если затылочные доли повреждены?
-
Предмет:
Биология -
Автор:
leoneldgbq - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Слово религия произошло от латинского слова:соединять,Бог,вера,всё правильно.
-
Какое определение понятия «дорога» приведено в Правилах дорожного движения
-
Предмет:
Обществознание -
Автор:
lucano - 6 лет назад
-
Ответов:
4 -
Смотреть
-
- Разложите на множители: 1-m2
How much to ban the user?
1 hour
1 day
100 years
