Задать вопрос Регистрация
Помочь другим

  • 30 БАЛЛОВ! Исследовать ряд на сходимость. Решите пожалуйста, буква а, и б. прилагаются фото

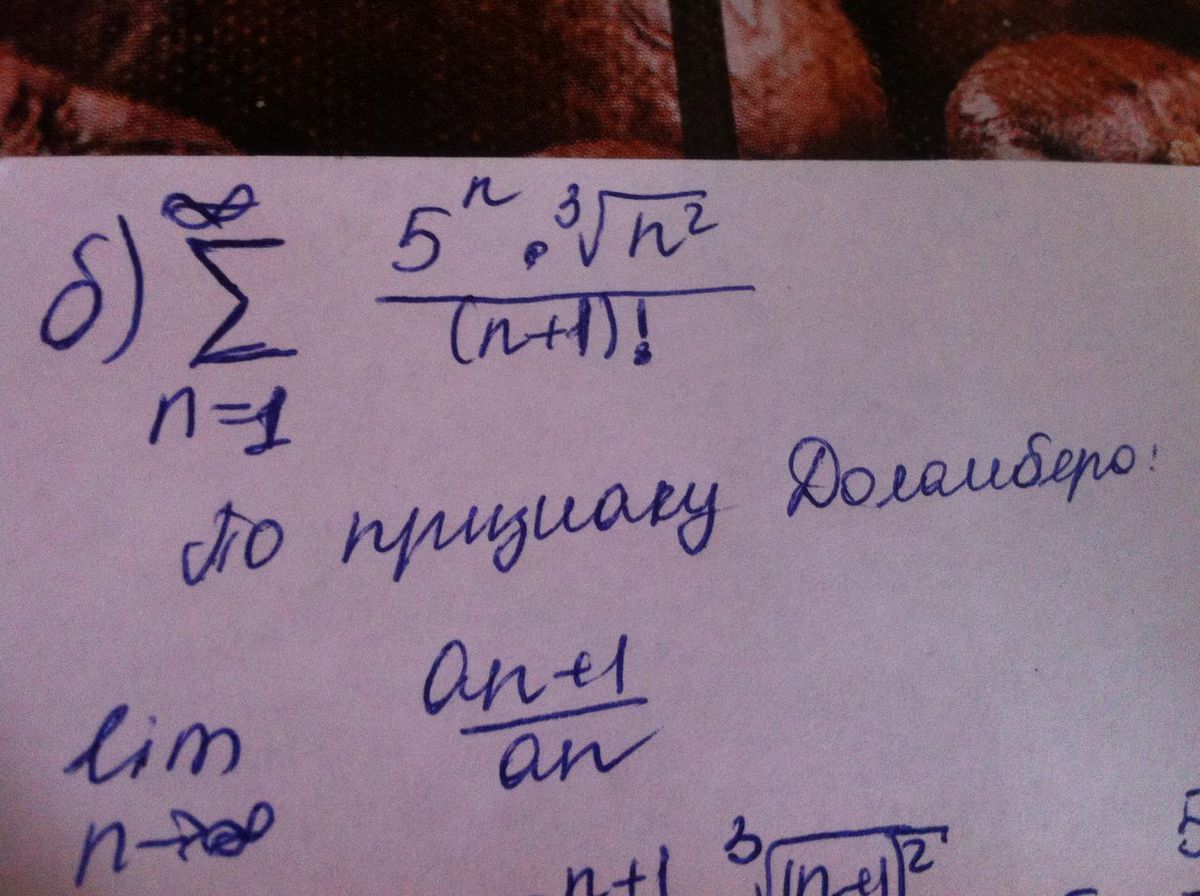
    question img
    question img

Ответы 2

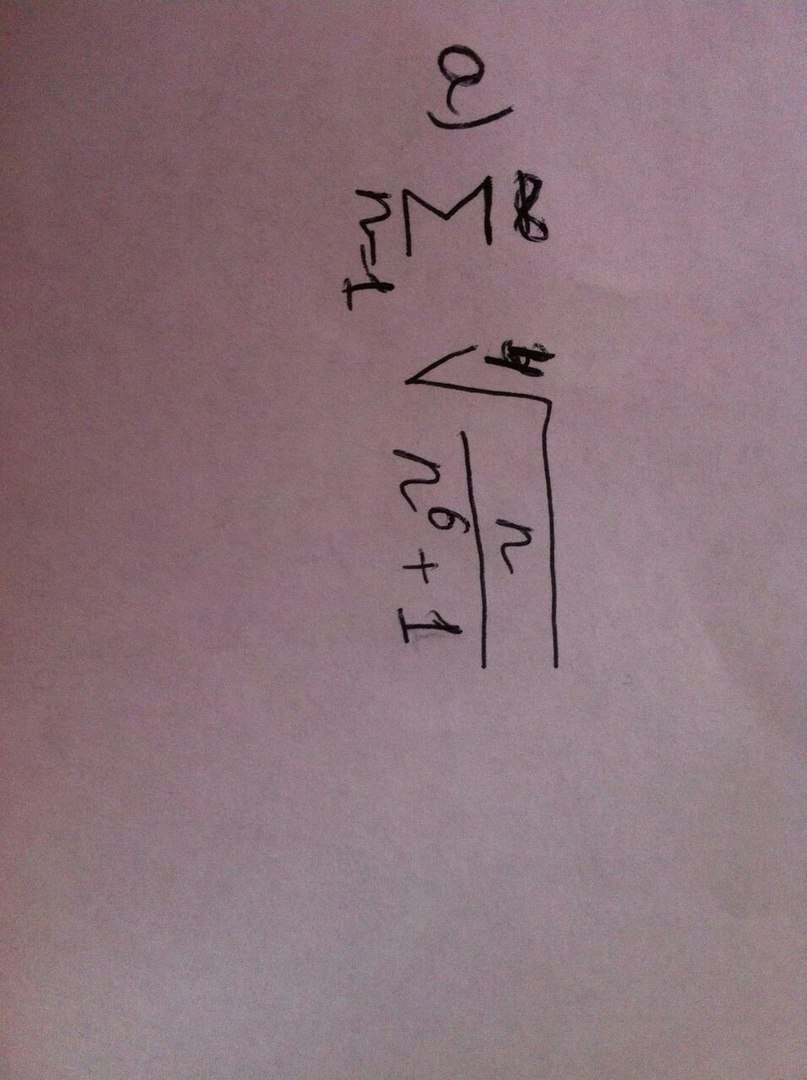
  • a)\Sigma \frac{1}{n^p} - обобщенный гармонический ряд,при p>1 - сходитсяпри p ≤ 1 - расходитсяДанный ряд эквивалентен ряду:\Sigma \sqrt[4]{ \frac{n}{n^6} }=\Sigma \sqrt[4]{ \frac{1}{n^5} } ==\Sigma \frac{1}{n^{ \frac{5}{4} }} 5/4 > 1 ряд сходится.Значит и данный ряд сходится.б) По признаку Даламбера: \lim_{n \to \infty} \frac{a_{n+1}}{a_n}= \lim_{n \to \infty} \frac{5^{n+1}\cdot \sqrt[3]{(n+1)^2}\cdot (n+1)!} {(n+2)!\cdot 5^n \cdot \sqrt[3]{n^2} }= \\ \\ = \lim_{n \to \infty} \frac{5}{n+2} \cdot \lim_{n \to \infty} \sqrt[3]{ (\frac{n+1}{n})^2 }=0\cdot1=0 0<1 по признаку Даламбера ряд сходится
  • 1)\; \; \sum \limits_{n=1}^{\infty }\sqrt[4]{ \frac{n}{n^6+1} } \; \sim \sum _{n+1}^{\infty }\frac{1}{\sqrt[4]{n^5}}=\sum _{n+1}^{\infty }\frac{1}{n^{5/6}}\; -\; sxoditsya,t.k.\; 5/4\ \textgreater \ 1\\\\\lim\limits _{n\to \infty }\frac{a_{n}}{b_{n}}=\lim\limits _{n\to \infty } \sqrt[4]{\frac{n}{n^6+1} }:\frac{1}{n^{5/4}}=1e 0\; \to \; oba\; sxodyatsya2)\; \sum _{n=1}^{\infty } \frac{5^{n}\sqrt[3]{n^2}}{(n+1)!} \\\\\lim\limits _{n\to \infty } \frac{a{n+1}}{a{n}} =\lim\limits _{n\to \infty } \frac{5^{n+1}\sqrt[3]{(n+1)^2}}{(n+2)!} : \frac{5^{n}\sqrt[3]{n^2}}{(n+1)!} =\\\\=\lim\limits _{n\to \infty } \frac{5^{n}\cdot 5\cdot (n+1)!\; \sqrt[3]{(n+1)^2}}{y5^{n}\cdot (n+1)!\cdot (n+2)\; \sqrt[3]{n^2}}=\lim\limits _{n\to \infty } \frac{5}{n+2}=[\frac{5}{\infty }]=0 \ \textless \ 1\; \Rightarrow \; sxod.

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years