40 баллов. 429 номер (два последних),внизу (если log 3 2l

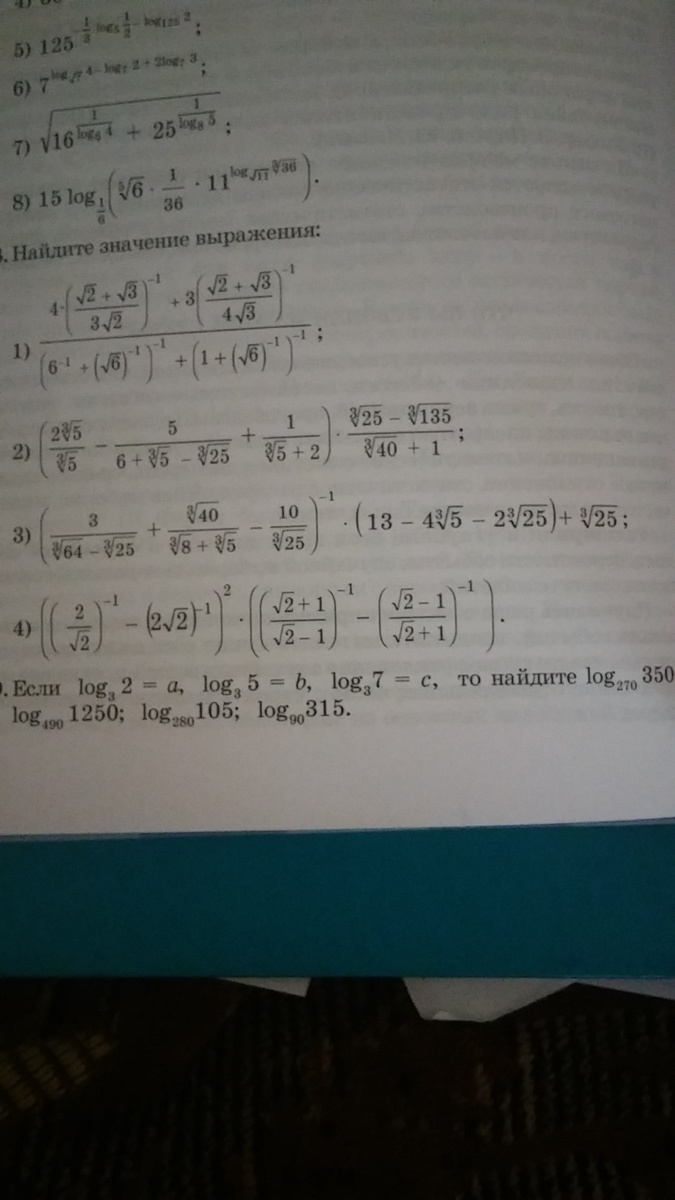
Ответы 2

Зато я в ТеХе набираю :)
- Автор:
  porkchopdougherty
- 6 лет назад
- 0
Привет :)Ничего, кроме свойств логарифма здесь использоваться не будет. Просто переходим к новому основанию и раскладываем на множители.Итак, нам известно следующее: $\log_32 = a, \ \log_35 = b, \ \log_37 = c. \\ a. \ \ \log_{280}{105} = \frac{\log_3{105}}{\log_3{280}} = \\ = \frac{\log_3{(3 \cdot 5 \cdot 7)}}{\log_3{(5 \cdot 7 \cdot 2^3 )}} = \frac{\log_33 + \log_35 + \log_37}{\log_35 + \log_37 + 3 \log_32 } = \\ = \frac{b + c +1}{3a+b+c }.$ Второе аналогично: $b. \ \ \log_{90}{315} = \frac{\log_3{315}}{\log_3{90}} = \\ = \frac{\log_3{(3^2 \cdot 5 \cdot 7)}}{\log_3{(3^2 \cdot 5 \cdot 2 )}} = \frac{2\log_33 + \log_35 + \log_37}{2\log_33 + \log_35 + \log_32 } = \\ = \frac{b + c +2}{a+b+2 }.$
- Автор:
  janiya
- 6 лет назад
- 0
Добавить свой ответ