-
Помогите, решить, пожалуйста!
Два однородных показательных неравенства.
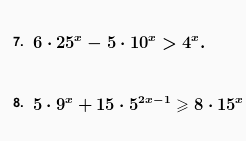
Ответы 1
-
1. 6*25^x-5*10^x>4^x
6*5^2x-5*2^x*5^x-2^2x>0
все разделим на 2^2x
6*(5/2)^2x-5*(5/2)^x-1=0
заменим (5/2)^x=t где t>0
тогда
6t^2-5t-1>0
D=25+24=49
t12=(5+-7)/12
t1=1
t2=-1/6 - не входит в область определения уравнения
функция больше нуля на участке от минус бесконечности до -1/6 и от 1 до бесконечности, оставляем только второй интервал
(5/2)^x>1
x>0
8. 5*9^x+15*5^(2x-1)>=8*15^x
5*3^2x+3*5^2x-8*5^x*3^x>=0 разделим все на 3^2x
5+3*(5/3)^2x-8*(5/3)^x>=0
заменим (5/3)^x=t
t>0
3t^2-8t+5>=0
D=16-15=1
t12=(4+-1)/3
t1=5/3
t2=1
больше 0 на участках t [-бесконечности до 1] и от [5/3 до +бесконечности]
но t всегда больше 0
тогда
[0;1] и [5/3 ;+бесконечности]
(5/3)^x=1 - х=0
(5/3)^x=5/3 - x=1
тогда х : [-бесконечности; 0] [1;+бесконечности]
-
Автор:
azariaandersen - 6 лет назад
-
0
-
-
Добавить свой ответ
-
В 2 книжных шкафах на каждой полке одинаковое количество книг.В первом шкафу 6 полок, во втором-8 полок и на 50 книг больше,чем в первом шкафу.сколько книг в каждом шкафу?
-
Предмет:
Математика -
Автор:
barr - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите плиз:*треугольник АВС и А1В1С1 равны,периметр треугольника АВС равен 105 см,а А1В1:В1С1:С1А1=4:5:6.найдите стороны треугольника АВС.
-
найдите 28 член арифм прогрессии -30,-28,-26
-
Предмет:
Алгебра -
Автор:
bookermcdonald - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Довжина алеі 540 м.Від двох кінців алеі одночасно назустріч один одному побігли Петрик та його песик.Через 2 хв. Петрик надів на песика новий повідок.З якою швидкістью біг Петрик,якщо швидкість песика була 15м\хв?
-
Предмет:
Математика -
Автор:
hanna2ng4 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
