-
Помогите с работой по алгебре)
Первый номер не надо.
Спасибо)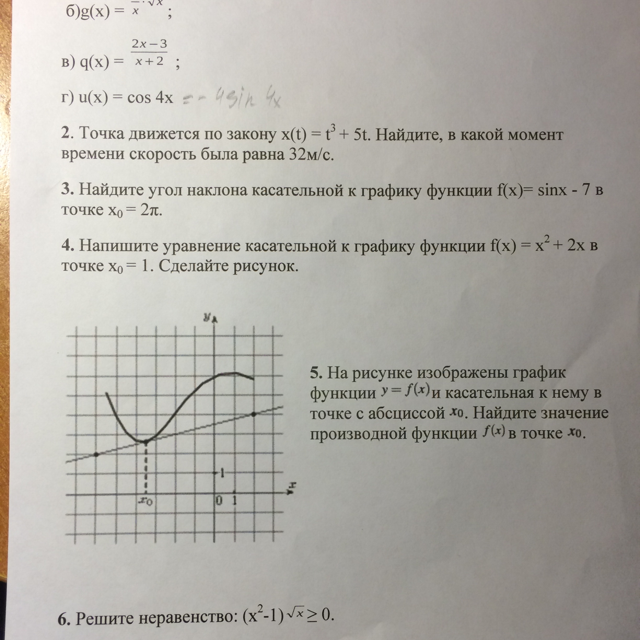
-
Предмет:
Алгебра -
Автор:
vincent536 - 6 лет назад
-
Ответы 1
-
2)x(t)=t^3+5t V=x'(t); (t^3+5t)'=3t^2+5; x'(t)=3t^2+5;V=3t^2+5; 3t^2+5=32; 3t^2=32-5;3t^2=27; t^2=9; t=3(t>0)3)f(x)=sinx-7; x0=2πtga=f'(2π); (sinx-7)'=cosx; f'(x)=cosx; f'(2π)=cos2π=1tga=1; a=π/4Ответ π/44) f(x)=x^2+2x; x0=1 y=f(x0)+f'(x0)(x-x0) f(x0)=f(1)=1+2=3;(x^2+2x)'=2x+2; f'(x)=2x+2; f'(1)=2*1+2=4y=3+4*(x-1); y=4x+3-4;y=4x-1-уравнение касательнойстроим 1)параболу f(x)=x^2+2xветви-вверхx^2+2x=0; x(x+2)=0; x=0 ili x=-2 (0;0) ; (-2;0)x=-1-абсцисса вершины; у=1+2*(-1)=-1; (-1;-1)-вершина параболы2)строим касательную; у=4х-1 по точкам (0;-1) и(2;7)5)k=f'(x0)=tgatga=2/4=1/2 (на рисунке гипотенуза прям тре-ка имеет концы в указанных точках) Считаем клетки! Отношение катета противолежащего углу к катету прилежащему=tgaf'(x0)=0,56)(x^2-1)√x≥0x≥0! (x^2-1)√x=0; x^2-1=0 ili x=0; x=+-1 ili x=0 - +---0-------1------------->x (1/2)^2-1)√1/2<0; ((2^2-1)√2)>0 ///////////////////Ответ [1;+∞)
-
Автор:
heathlrya - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите поставить правильно запятые "Спустя месяц мы наконец-то это собрали"
-
Предмет:
Русский язык -
Автор:
benson32 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Определите координаты точки касания касательной к графику функции f(x)=4x+3x^2,если угловой коэффициент касательной равен 22.
-
Предмет:
Алгебра -
Автор:
bumpkinfsvf - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
1) В Красную книгу Карелии занесено 57 видов рыб. Округлите число до десятков.
2) В Красную книгу Карелии занесено 31 вид насекомых. Округлите число до десятков.
3) В Красную книгу Карелии занесено 1100 видов цветковых растений. Округлите число до тысяч.
4) В Красную книгу Карелии занесено 280 видов птиц. Округлите число до сотен.
5) В Карелии 95 памятников природы, 2 национальных парка, 2 заповедника. Сколько особо
охраняемых территорий в нашей республике? Округлите это число до сотен-
Предмет:
Математика -
Автор:
roryii1b - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
округли до десятков тысяч 6790043
-
Предмет:
Математика -
Автор:
rolliez87p - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
