-
Объясните как преобразовали !!! Пожалуйста, можете расписать решение
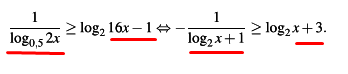
Ответы 7
-
и как это из неравенства получилось уравнение?
-
Автор:
mouse15 - 6 лет назад
-
0
-
-
числитель не может быть < 0
-
Автор:
winston - 6 лет назад
-
0
-
-
уравнение то никак из этого не получится))
-
Автор:
redot91 - 6 лет назад
-
0
-
-
зато знаменатель может быть < 0
-
Автор:
jordenkn3q - 6 лет назад
-
0
-
-
так оно и есть
-
Автор:
maxwellmendoza - 6 лет назад
-
0
-
-
- - +_____________[-2]__________(-1)___________t∈(-∞;-1)log₂x<-1 ОДЗ: x>0log₂x<log₂(1/2)2- основание логарифма, 2>1, следовательноx<1/2С учётом ОДЗ получаем 0<x<1/2Ответ: (0; 1/2)
-
Автор:
figgylmxc - 6 лет назад
-
0
-
-
решение смотри во вложении

-
Автор:
victoria31 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
помогите плиз,взаимодействие воды с металлами, с основными оксидами и с кислотными оксидами +реакции
-
Предмет:
Химия -
Автор:
ubaldohines - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Докрасна завидно прозорливо донизу в каком слове ударение на второй слог
-
Предмет:
Русский язык -
Автор:
nicolas960 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
чтобы сшить 7 одинаковых костюмов нужно 28 метров ткани сколько таких костюмов можно сшить из 960 метров ткани
-
Предмет:
Математика -
Автор:
angel100 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Срочно люди!!! Помогите пожалуйста!!! Плииииз плиииз!!!!! Биология 9 класс лабораторная работа, ном8. Про хлопчатник задача!!!!
-
Предмет:
Биология -
Автор:
embermckinney - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
