-
Ребят, просьба помочь решить 10 тригонометрических уравнений.Ошибаться нельзя-решается судьба годовой оценки.
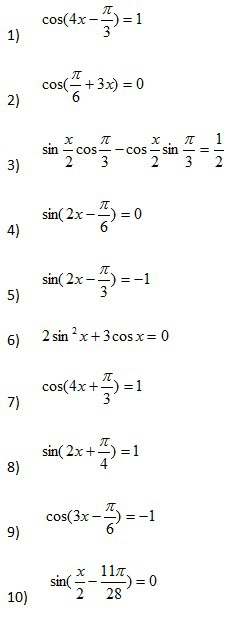
-
Предмет:
Алгебра -
Автор:
shadowgiyn - 6 лет назад
-
Ответы 2
-
Извините, но в 10 (sin x/2-11п/28), но всё равно спасибо вам большое!
-
Автор:
dillon - 6 лет назад
-
0
-
-
1)Cos(4x - π/3) = 14x - π/3 = 2πk, k ∈Z4x = 2πk + π/3, k ∈Zx = πk/2 + π/12, k∈Z2)Cos(π/6 +3х) = 0π/6 +3х = π/2 + πk , к ∈Z3x = π/2 + πk - π/6, k ∈Z3x = π/3 + πk, k ∈Zx = π/9 + πk/3, k ∈Z3)Sin(x/2 - π/3) = 1/2х/2 - π/3 = (-1)^n arcSin1/2 + nπ, n ∈Z'x/2 -π/3 = (-1)^n π/6 + πn, n ∈Zx/2 = (-1)^n π/6 + πn + π/3, n ∈Zx = (-1)^n π/3 + 2πn + 2π/3 , n ∈Z4)Sin(2x - π/6) = 02х - π/6 = nπ, n ∈Z2x = nπ + π/6, n∈Zx = nπ/2 + π/12, n ∈Z5)Sin(2x -π/3) = -12х - π/3 = -π/2 + 2πk ,к ∈Z2x = π/3 -π/2 + 2πk, k ∈Zx = π/6 -π/4 + πk, k ∈Z6) 2Sin² x +3Cosx = 02(1-Cos²x) + 3Cosx = 02 - 2Cos²x + 3Cosx = 02Cos²x -3Cosx - 2 = 0 Решаем как квадратноеа)Соs x = 2 (нет решений)б) Сos x = -1/2х = +-arcCos(-1/2) + 2πk, k ∈Zx = +- 2π/3 + 2πk, k ∈Z7)Cos(4x + π/3) = 14x + π/3 = 2πk, k ∈Z4x = 2πk - π/3, k ∈Zx = πk/2 - π/12, k∈Z8) Sin(2x + π/4) = 12х + π/4 = π/2 + 2πк, к ∈Z2x = -π/4 +π/2 + 2πк, к ∈Zx = -π/8 + π/4+ πк, к ∈Z9) Cos(3x - π/6) = -13x - π/6 = π + 2πк , к ∈Z3x = π/6 + π + 2πк , к ∈Z3x =7π/6 + 2πк , к ∈Zx = 7π/18 +2πк/3, к ∈Z10) Sin(x/2 + 11π/28) = 0х/2 + 11π/28 = nπ, n ∈Zx/2 = nπ - 11π/28, n∈Zx =2 nπ - 11π/14, n ∈Z
-
Автор:
heriberto - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Вычисли значения выражений и сделай проверку и столбик 760760:364
-
Предмет:
Математика -
Автор:
cumulus7mwm - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Решите неравенство x^2-81<=0
-
Предмет:
Алгебра -
Автор:
arabellakoch - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
найдите трёхзначное число А, обладающее всеми свойствами:
- сумма цифр числа А делится на 12;
- сумма цифр числа А плюс 6 делится на 12.
в ответе укажите какое-нибудь одно число.-
Предмет:
Математика -
Автор:
roxannetiq5 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Тело массой 0, 5 кг. брошено вверх со скоростью 30 м/с. Чему равна работа, которую совершает сила тяжести: при подъеме на максимальную высоту; при его падении до первоначального уровня?
How much to ban the user?
1 hour
1 day
100 years
