Помогите, пожалуйста, решить данный пример. У меня в ответе нет корней. Может у Вас

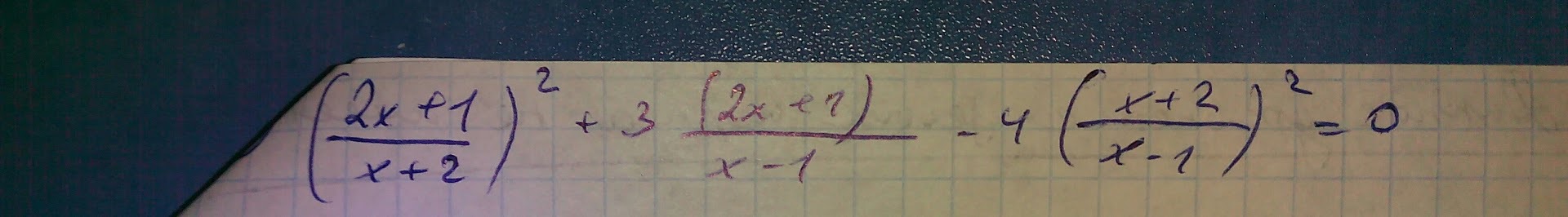
Ответы 1

Надо заметить следующее $\frac{2x+1}{x+2} * \frac{x+2}{x-1} = \frac{2x+1}{x-1}$ Значит это уравнение можно переписать $( \frac{2x+1}{x+2} ) ^{2}+3 \frac{2x+1}{x+2}* \frac{x+2}{x-1} -4 (\frac{x+2}{x-1})^{2}=0$ ОДЗ: х≠-2; х≠1пусть $\frac{2x+1}{x+2} =a;\frac{x+2}{x-1}=b$ тогда уравнение примет вид:a²+3ab-4b²=0- однородное уравнение второй степени $a ^{2}+3ab-4b ^{2} =0 |:b ^{2} \\ ( \frac{a}{b} )^{2} +3 \frac{a}{b} -4=0$ и снова делаем заменупусть $\frac{a}{b} =t \\ t^{2} +3t-4=0 \\ t=-4 \\ t=1$ 1) $\frac{a}{b} =-4 \\ \frac{2x+1}{x+2}: \frac{x+2}{x-1}=-4 \\ \frac{2x+1}{x+2}*\frac{x-1}{x+2}=-4 \\ \frac{2 x^{2}-x-1 }{(x+2) ^{2} } =-4|*(x+2) ^{2} \\ 2 x^{2} -x-1=-4( x^{2} +4x+4) \\ 2 x^{2} -x-1=-4 x^{2} -16x-16 \\ 6 x^{2} +15x+15=0 \\ D\ \textless \ 0$ 2) $\frac{a}{b} =1 \\ a=b \\ \frac{2x+1}{x+2}= \frac{x+2}{x-1} \\ (x+2) ^{2} =(2x+1)(x-1) \\ x^{2} +4x+4=2 x^{2} -x-1 \\ x^{2} -5x-5=0 \\ D= 25+4*5=45 \\ \sqrt{D} = \sqrt{45} =3 \sqrt{5} \\ x= \frac{5+3 \sqrt{5} }{2} \\ x=\frac{5-3 \sqrt{5} }{2}$
- Автор:
  tabby
- 5 лет назад
- 0
Добавить свой ответ