-
Используя метод математической индукции, докажите, что при любом натуральном n
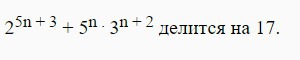
Ответы 2
-
1) проверяем справедливость при n=1.
верно.2) предполагаем что утверждение верно для n, тогда оно будет верно и для (n+1). Проверяем.
1 слагаемое суммы делиться на 17, т.к. содержит такой множитель.2 слагаемое суммы тоже делится на 17, т.к. выражение в скобках делится на 17(по нашему предположению).Значит и сумма делится на 17.Согласно методу мат. индукции это будет справедливо для любых натуральных n.
-
Автор:
kierstengilmore - 6 лет назад
-
0
-
-
==========================================>>>>+++

-
Автор:
carson - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Решите неравенство: log5(3x+1)-log5(x-2)<= 0
-
Предмет:
Математика -
Автор:
konnorhayden - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В отличие от неорганических веществ большинство органических веществ
1) Тугоплавки
2) Легкоплавки
3) Нелетучи
4) Электролиты
5) Негорючи-
Предмет:
Химия -
Автор:
dandyhopkins - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Ребяяяяяяят
Пожалуйста
6 задание
Умоляяяяяяю вас-
Предмет:
Алгебра -
Автор:
hammerpdhh - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Визначте тип мутації ТГАГАЦАГАТТАЦ => ТГАГАЦАГТТГААТТАЦ
-
Предмет:
Биология -
Автор:
emilianobecker - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
