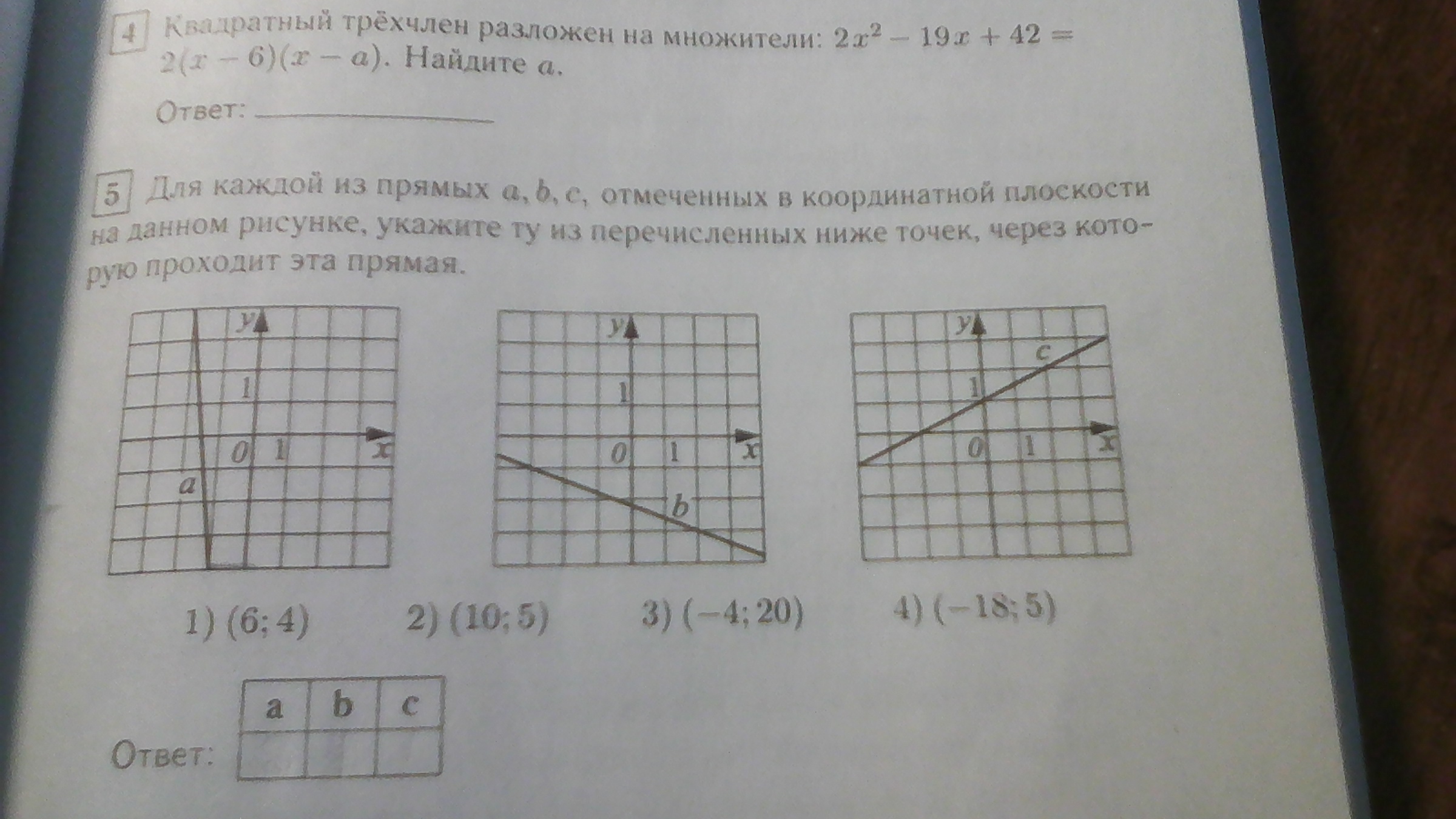
Решите пожалуйста с объяснением.Я не понимаю как это решать.Пожалуйста.Номер 5.

Находим уравнение каждой прямой по формуле (х-х1)/(х2-х1)=(y-y1)/(y2-y1).Потом подставляем в уравнение каждую из точек и находим равенство

Надо выделить "узловые" точки, через которые проходит каждая прямая.(Точки с целочисленными координатами) см. рисунок в приложении.Написать уравнение каждой прямой, как прямой проходящей через эти точки по формуле:(x-x₁)/(x₂-x₁)=(y-y₁)/(y₂-y₁)В итогепрямая а(х+2)/(-1+2)=(у-4)/(-4-4)  или  8х+у+12=0прямая b(x+3)/(2+3)=(y+1)/(-3+1)  или  2х+5у+11=0прямая су=кх+bb=1k=1/2Чтобы проверить, принадлежит ли точка прямой надо подставить координаты этой точки в уравнение  прямой.Поскольку точек четыре, то  первая прямая точно не проходит через точки 1),2) и 4)см. рис. 2Поэтому остается проверить только точку 3) с координатами (-4;20)х=-4  у=208·(-4)+20+12=0 - ВЕРНО, 0=0О т в е т. 3)точка (-4;20) принадлежит  прямой а.Прямой b точно не принадлежит точка (6;4); (10;5) и (-4;20), осталось проверить точку 4) с координатами (-18;5)х=5 у=-182·(-18)+5·5+1=0 - ВЕРНО.  0=0О т в е т. 4)точка (-18;5) принадлежит  прямой b.Прямой с могут принадлежать точки 1) или 2)х=6  у=44=0,5·6+1- верно,х=10 у=55=0,5·10+1 - неверно.Ответ. прямой с принадлежит точка 1) (6;4)