Задать вопрос Регистрация
Помочь другим

  • Найдите среднее арифметическое всех корней уравнения

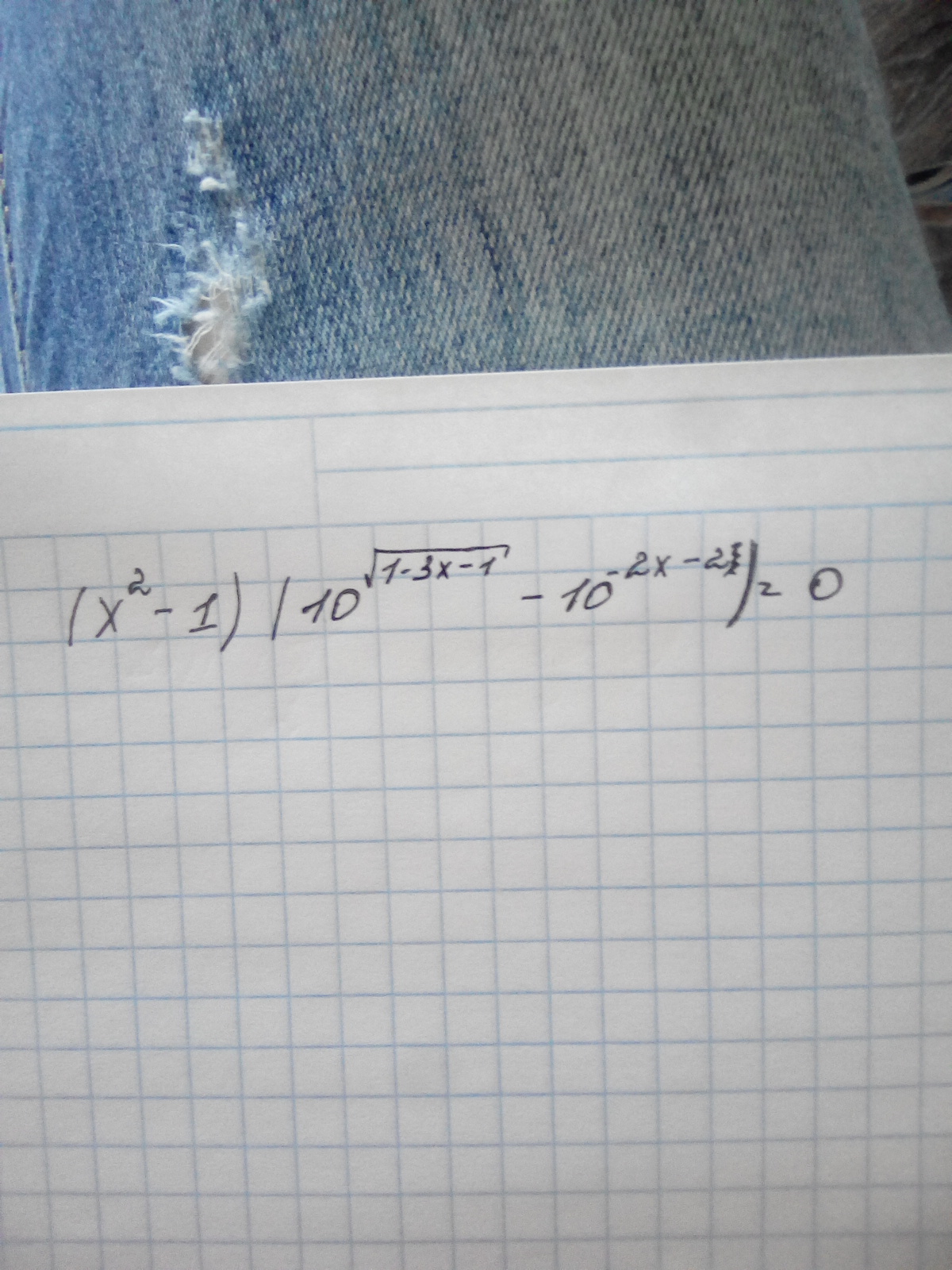
    question img

Ответы 1

  • (x^2-1)(10^{ \sqrt{1-3x-1} }-10^{-2x-2})=0(x^2-1)(10^{ \sqrt{-3x} }-10^{-2x-2})=0Найдем ОДЗ уравнения. -3x \geq 0 откуда x \leq 0Произведение равно нулю, значит имеем 2 уравненияx^2-1=0\\ x=\pm 1и10^{ \sqrt{-3x} }-10^{-2x-2}=0\\ 10^{ \sqrt{-3x} }=10^{-2x-2}\\ \sqrt{-3x}=-2x-2\\ -3x=4x^2+8x+4\\ 4x^2+11x+4=0Дальше решается как квадратное уравнение. D=b^2-4ac=11^2-4\cdot4\cdot4=57\\ \\ x_1= \frac{-b+ \sqrt{D} }{2a} = \frac{-11+ \sqrt{57} }{8} \\\\ x_2=\frac{-b- \sqrt{D} }{2a} = \frac{-11- \sqrt{57} }{8} корни x=\frac{-11+\sqrt{57} }{8} и x=1 не удовлетворяют ОДЗ.Среднее арифметическое всех корней уравнения:  \frac{\frac{-11- \sqrt{57} }{8}-1}{2} = \frac{-11- \sqrt{57} -8}{16} =\frac{-19- \sqrt{57} }{16}

    • Автор:

      roryii1b
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years