Задать вопрос Регистрация
Помочь другим

  • sin(2α)/(1+cos(2α)) *cosα/(1+cos(α))* cos(α/2)/((1+cosα/2).
    ребят, скажите у кого как выходит я помешала вышел ответ как на втором фото ,правильно ли?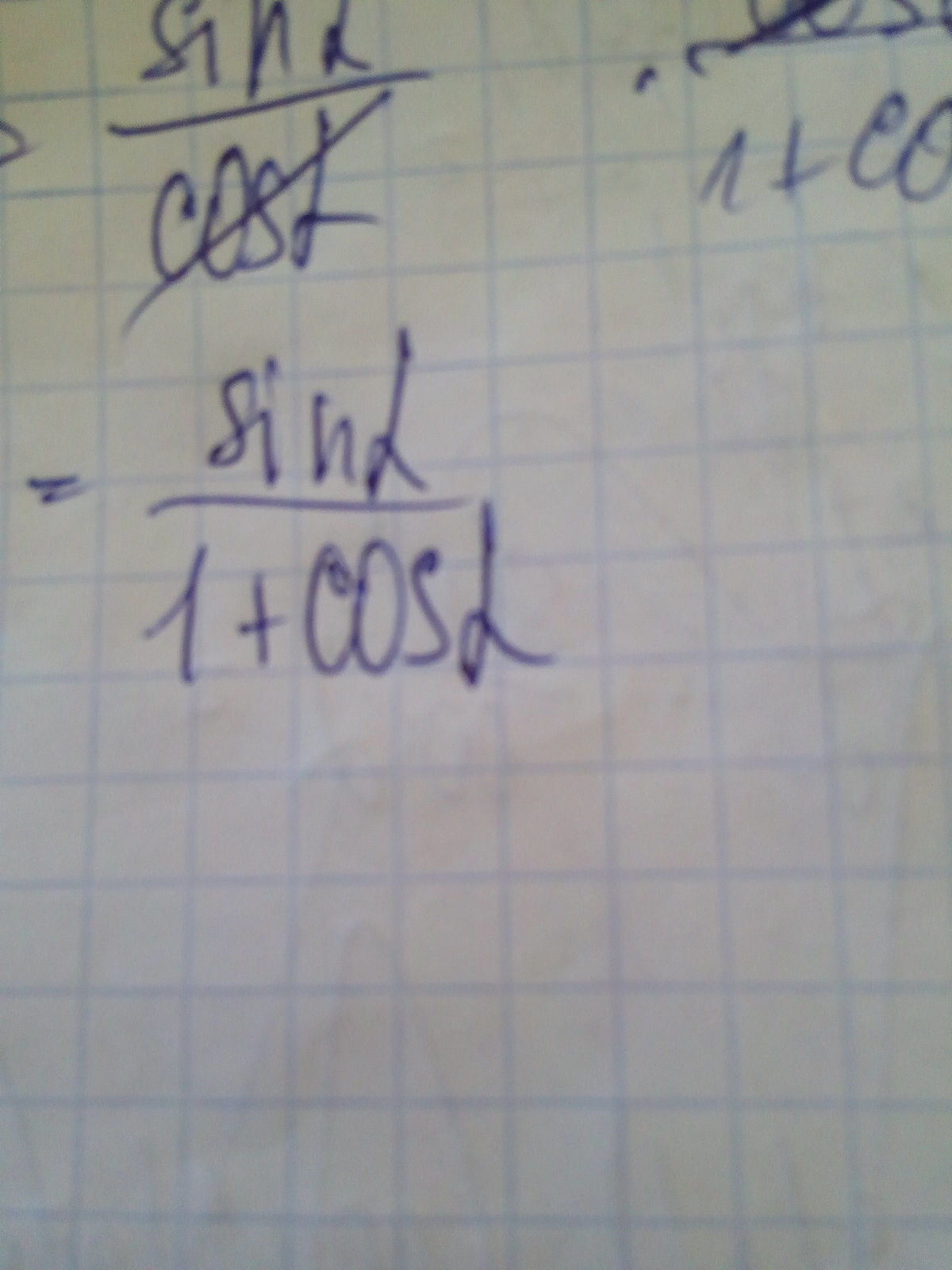

    question img

Ответы 1

  • \frac{sin2 \alpha }{1+cos2 \alpha } \cdot \frac{cos \alpha }{1+cos \alpha } \cdot \frac{cos\frac{ \alpha }{2}}{1+cos\frac{ \alpha }{2}}= \frac{2sin \alpha \cdot cos \alpha }{1+(2cos^2 \alpha -1)} \cdot \frac{cos \alpha }{1+cos \alpha } \cdot \frac{cos\frac{ \alpha }{2}}{1+cos\frac{ \alpha }{2}} = =\left (\frac{sin \alpha }{cos \alpha }\cdot \frac{cos \alpha }{1+cos \alpha }ight )\cdot \frac{cos\frac{ \alpha }{2}}{1+cos\frac{ \alpha }{2}} =  \frac{sin \alpha }{1+cos \alpha } \cdot \frac{cos\frac{ \alpha }{2} }{1+cos\frac{ \alpha }{2}}==\frac{sin\frac{ \alpha }{2}}{cos\frac{ \alpha }{2}}\cdot \frac{cos \frac{ \alpha }{2} }{1+cos \frac{ \alpha }{2} } = \frac{sin\frac{ \alpha }{2}}{1+cos \frac{ \alpha }{2} } =tg\frac{ \alpha }{4}\\\\Formyla:\quad \frac{sinx}{1+cosx} =tg\frac{x}{2}\; \left (=\frac{sin\frac{x}{2}}{cos\frac{x}{2}}\; ight )

    • Автор:

      wallace
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years