Решите - №19198233

Решите неравенство
..................................................................
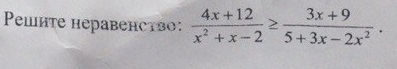
- Предмет:
  Алгебра
- Автор:
  chocolatebishop
- 5 лет назад

Ответы 2

Спасибо
- Автор:
  mackenziejaum
- 5 лет назад
- 0
$\frac{4x+12}{x^2+x-2} \geq \frac{3x+9}{5+3x-2x^2}$ $\frac{4x+12}{x^2+x-2} -\frac{3x+9}{5+3x-2x^2} \geq 0$ $\frac{4x+12}{x^2+x-2} -\frac{3x+9}{-(2x^2-3x-5)} \geq 0$ $\frac{4x+12}{x^2+x-2}+\frac{3x+9}{2x^2-3x-5} \geq 0$ $x^2+x-2=0$ $D=1^2-4*1*(-2)=1+8=9$ $x_1= \frac{-1+3}{2}=1$ $x_2= \frac{-1-3}{2}=-2$ $x^2+x-2=(x-1)(x+2)$ $2x^2-3x-5=0$ $D=(-3)^2-4*2*(-5)=9+40=49$ $x_1= \frac{3+7}{4}=2.5$ $x_2= \frac{3-7}{4}=-1$ $2x^2-3x-5=2(x-2.5)(x+1)$ $\frac{4(x+3)}{(x-1)(x+2)}+\frac{3(x+3)}{2(x-2.5)(x+1)} \geq 0$ $\frac{4(x+3)(2x^2-3x-5)+3(x+3)(x^2+x-2)}{(x-1)(x+2)(2x-5)(x+1)} \geq 0$ $\frac{(x+3)(4(2x^2-3x-5)+3(x^2+x-2))}{(x-1)(x+2)(2x-5)(x+1)} \geq 0$ $\frac{(x+3)(8x^2-12x-20+3x^2+3x-6)}{(x-1)(x+2)(2x-5)(x+1)} \geq 0$ $\frac{(x+3)(11x^2-9x-26)}{(x-1)(x+2)(2x-5)(x+1)} \geq 0$ $11x^2-9x-26=0$ $D=(-9)^2-4*11*(-26)=81+1144=1225=35^2$ $x_1= \frac{9+35}{22}=2$ $x_2= \frac{9-35}{22}=- \frac{13}{11} =-1 \frac{2}{11}$ $11x^2-9x-26=11(x-2)(x+1 \frac{2}{11} )$ $\frac{(x+3)*11(x-2)(x+1 \frac{2}{11} )}{(x-1)(x+2)(2x-5)(x+1)} \geq 0$ $\frac{(x+3)(x-2)(11x+13 )}{(x-1)(x+2)(2x-5)(x+1)} \geq 0$ - + - + - + - + --------[-3]--------(-2)--------[-1 2/11]-------(-1)-------(1)--------[2]--------(2.5)------ ////////// //////////// /////////// //////// $x$ ∈ $[-3;-2)$ ∪ $[-1 \frac{2}{11} ;-1)$ ∪ $(1;2]$ ∪ $(2.5;+$ ∞ $)$
- Автор:
  felipeeeuj
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

Решите уравнения 1) -х²+3х+55=(х+7)² 2) (х-7)²=2х²+11х+23
- Предмет:
  Алгебра
- Автор:
  claudiogibson
- 5 лет назад
- Ответов:
  
  1
- Смотреть
Ex.4 Заполните пропуски и задайте специальные вопросы. Предложения переведите.

5. My favourite season … summer. – What …? 6. Summer … bright and nice. – Why…? 7. His birthday … in January. – When …? 8. It … August. – What month…? 9. The children … in the str
- Предмет:
  Английский язык
- Автор:
  leia
- 5 лет назад
- Ответов:
  
  1
- Смотреть
разложить на множители ;
A^2 * y^2 - X^6
помогите пожалуйста
- Предмет:
  Математика
- Автор:
  mario297
- 5 лет назад
- Ответов:
  
  2
- Смотреть
Помогите очень надо!!!

Подобные слагаемые. Раскрытие скобок

1. Раскройте скобки и найдите значение выражения.

23,4- (-5,6 + 7,4) + (-13,6 -1)

2. Приведите подобные слагаемые.

а) 4х + 12а – 6х – 12а

б) -13 + 4а – 6 – 8а + а

3. Упростите.
а) -3а ∙(-2,2х)
б) 3(2х – 9) – 4(-3х + 2)
в) -3,5 ∙ (4а – 2х) + (-3а – 5,2х)
г) 0,9(0,4 – х) – 0,2(0,8 – 4,5х)

4. Найдите значение выражения.

2(5а – 4х) – 3(4а – х), если а = -5 и х = 0,8

5. Решите уравнение.

3(0,4х + 7) – 4(0,8х – 3) = 2
- Предмет:
  Математика
- Автор:
  campos
- 5 лет назад
- Ответов:
  
  1
- Смотреть

How much to ban the user?

1 hour 1 day 100 years