-
Пример номер 376
Корни нашла, но не могу понять что делать дальше с неравенствами под цифрами 1-4
Помогите пожалуйста!!!!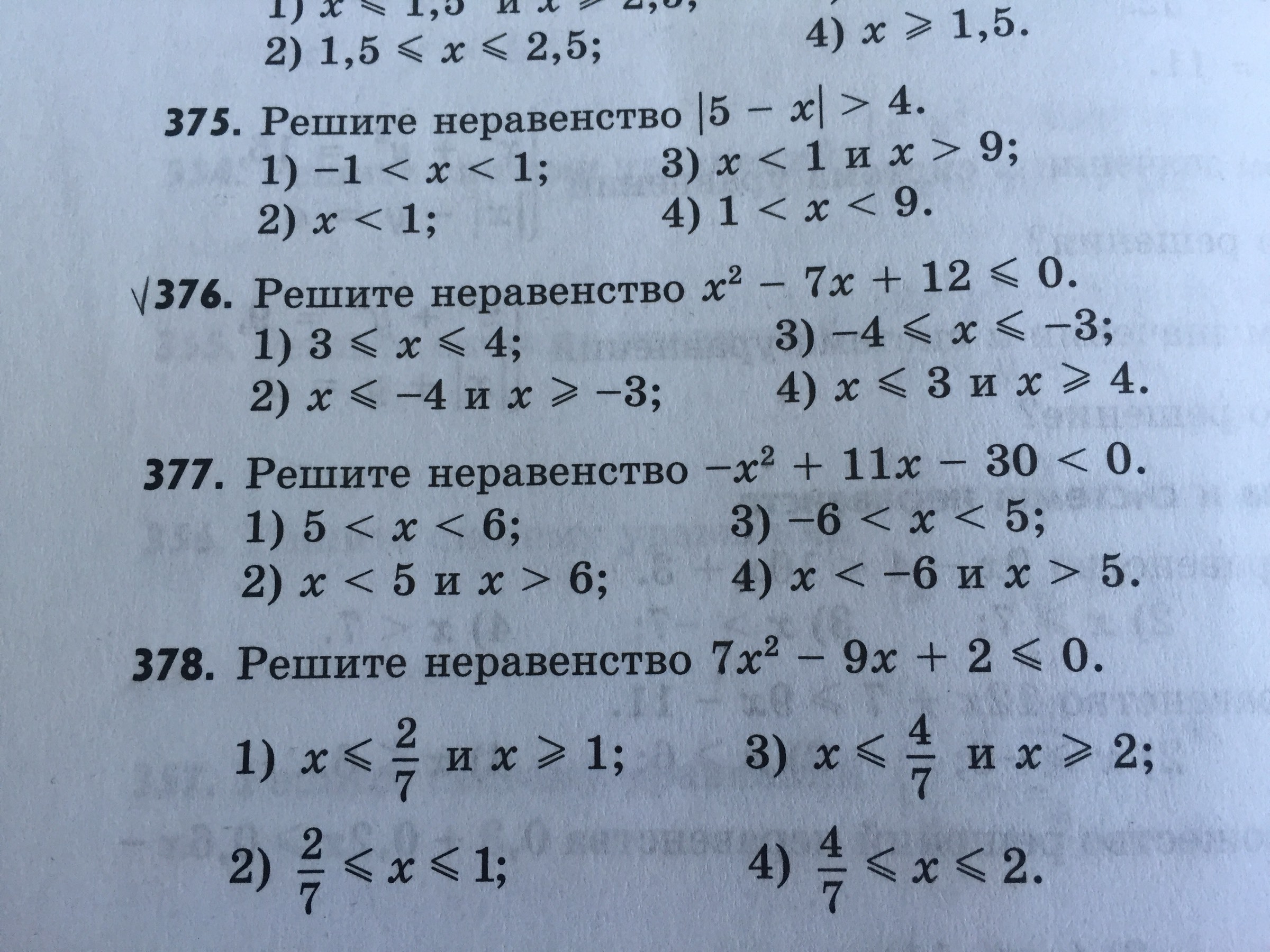
Ответы 4
-
я понимаю как решать, не понимаю что делать с примерами ниже под цифрами 1-4
-
Автор:
venanciofqxq - 6 лет назад
-
0
-
-
Это возможные варианты ответов. Надо выбрать правильный. Правильный 1)
-
Автор:
maribel - 6 лет назад
-
0
-
-
Можно решать методом интервалов.Находим нули функции у=х²-7х+12.х²-7х+12=0D=(-7)²-4·12=49-48=1x=(7-1)/2=3 или х=(7+1)/2=4Эти точки разбивают числовую прямую на три промежутка________[3]_____[4]__________График любой функции переходя из верхней полуплоскости в нижнюю проходит через нуль ( точку пересечения с осью ох).Поэтому если в какой-то точке интервала значение функции положительно, то оно положительно на всем интервале.Находим знак в точке 10, например, у(10)=10²-7·10+12 >0, значит на [4;+∞) функция принимает положительные значения, ставим +.________[3]_____[4]____+______Далее знаки чередуем.___+____[3]__-__[4]____+______О т в е т. x∈[3;4] или 3≤х≤4; это ответ под номером 1).Можно решать графически.Графиком функции у=х²-7х+12 является парабола. Ветви параболы направлены вверх. См. рисунок в приложенииПарабола пересекает ось ох в двух точкахх=3 и х=4.На (-∞;3] и на [4;+∞) парабола расположена выше оси Ох.Значит выполняется неравенствох²-7х+12 ≥0На [3;4] парабола расположена ниже оси Ох.Значит выполняется неравенствох²-7х+12≤0О т в е т. x∈[3;4] или 3≤х≤4; это ответ под номером 1).

-
Автор:
jettazkys - 6 лет назад
-
0
-
-
нам вбивала учительница: корни->парабола->ответ

-
Автор:
monica - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Я бы хотела иметь такого друга как пепе длинный чулокпотому что
-
Предмет:
Литература -
Автор:
albamartin - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите решить!
4x+4y = 16
5×(x+y) = 20-
Предмет:
Математика -
Автор:
rosendomclaughlin - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В чем проявляется опасность некоторых простейших животных для человека?
-
Предмет:
Биология -
Автор:
slinkykboy - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Имеют ли эти элементы летучик водородные соединения и почему?
Fe,Cs,Be-
Предмет:
Химия -
Автор:
junecarson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
