-
Найти производные.
С разъяснением, пожалуйста.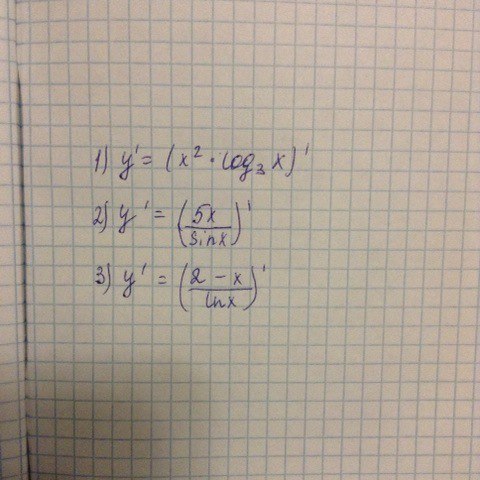
-
Предмет:
Алгебра -
Автор:
amiyahaspn - 6 лет назад
-
Ответы 1
-
-
Автор:
hampton - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
как решать покажите или решите я посмотрю как решать 20задачу
-
Предмет:
Алгебра -
Автор:
commandofields - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- как в условиях абсолютизма были организованы армия налоги экономика
-
Оксиды, основания, соли, кислоты вот это всё. Объясните, желательно на простейшем языке как для дошкольника, как это решается, спасибо.
K2O+HCL=
So2+KOH=
LiOH+CO2=
LiOH+HCL=
LIOH+SO3=
H3Po4+K=
H3PO4+NA2O=
H3Po4+LiOH=
H3PO4+AgNO3=
CuCL2+Fe=
CuCL2+NaOH=
CuCL2+AgNO3=-
Предмет:
Химия -
Автор:
crespotix5 - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
трактористу поручено вспахать поле.половину поля тракторист вспахивал с производительностью 12 га/ч. потом повысил производительность на 25%.сколько в среднем гектаров вспахивал тракторист за час
-
Предмет:
Математика -
Автор:
jasmine42 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
