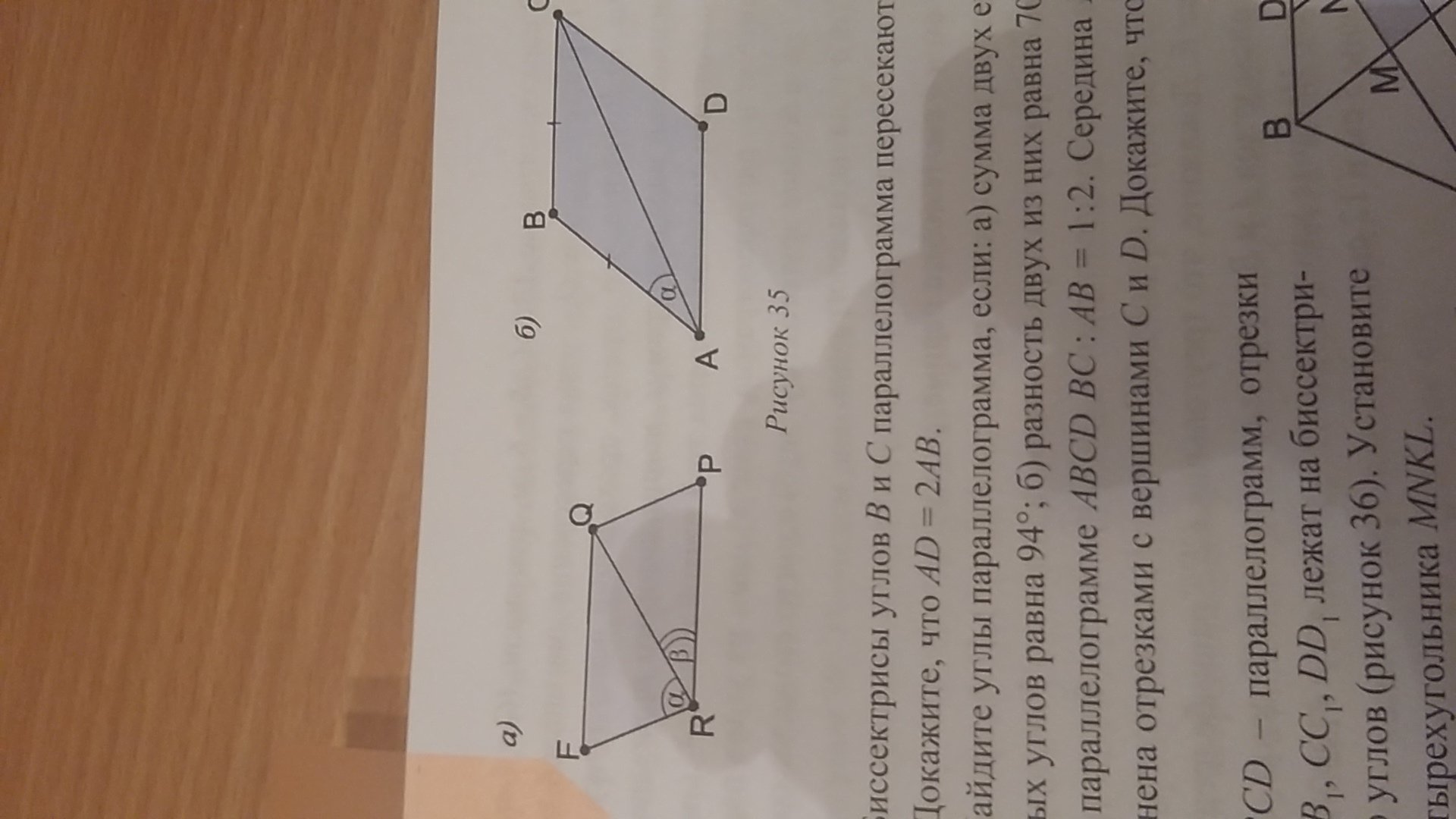
ПО ДАННЫМ НА РИСУНКЕ 35 А,Б, НАЙДИТЕ А) УГЛЫ ПАРАЛЛЕЛОГРАММА RFQP б)углы параллелограмма АВСD и докажите, что он является ромбом . СРОЧНО Рисунок 35 хорошо виден

а) RFQP - параллелограмм по условию, а значит, FQ || RP, так как противолежащие стороны параллелограмма равны и параллельны. FR - секущая, ∠RFQ и ∠FRP - односторонние в этом случае, а сумма односторонних углов равна 180°. ∠FRQ + ∠QRP = α + β; ∠RFQ = 180°-(α+β)

∠FQR = ∠FRP = α+β; ∠QFR = ∠QPR = 180°-(α+β)

б) ABCD - параллелограмм по условию, то есть у него противолежащие стороны равны. Но по условию видно, что и смежные стороны равны. А если это так, то у параллелограмма все стороны равны, а значит, это ромб. Теперь найдем углы ромба.

ΔABC - равнобедренный, ∠BAC=∠ACB (углы при основании равнобедренного треугольника), ∠ABC=180°-(α+α)=180°-2α

Параллелограмм - симметричная фигура относительно любой диагонали, так что в нижнем треугольнике все соответственные элементы равны.

∠BAC=∠CAD=α; ⇒∠BAD=∠BAC+∠CAD=α+α=2α;

∠BCD = ∠BAD=2α; ∠ADC=∠ABC=180°-2α