помогите плиз решить!!!! Докажите, что заданное множество состоит из одного числа

помогите плиз решить!!!!
Докажите, что заданное множество состоит из одного числа (элемента) и найдите это число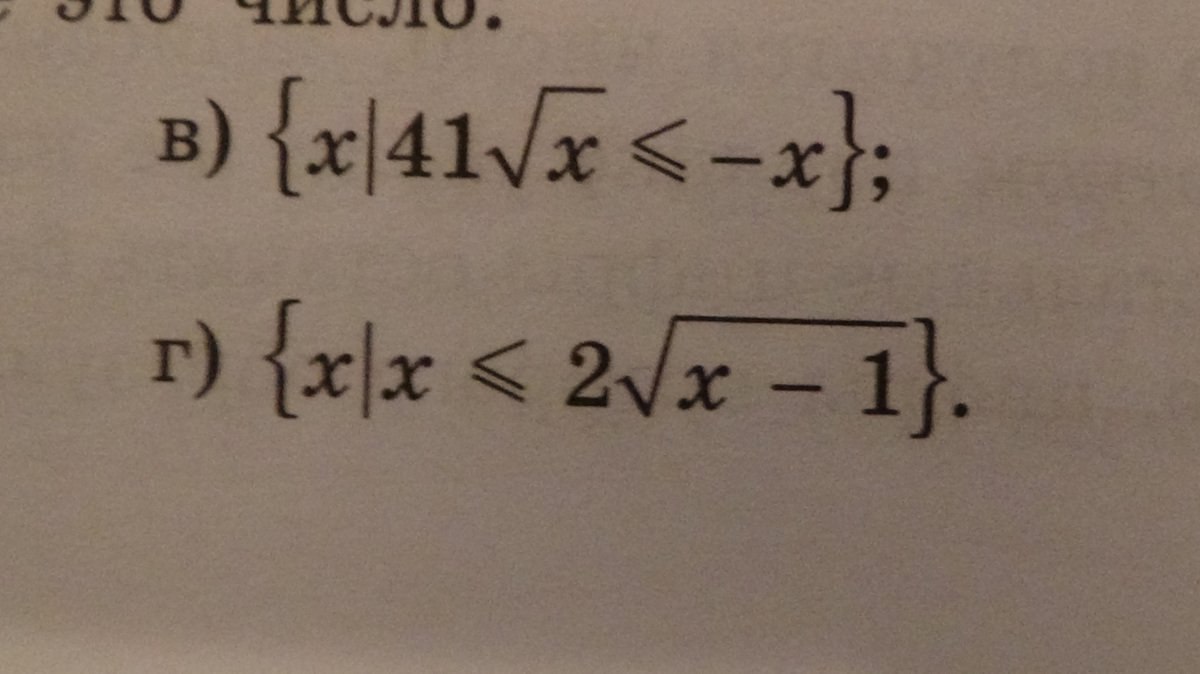
- Предмет:
  Алгебра
- Автор:
  claire
- 5 лет назад

Ответы 2

$\{x\ |\ 41 \sqrt{x} \leq -x\}$ $41 \sqrt{x} \leq -x$ $\sqrt{x} \leq - \frac{x}{41}$ $\left\{\begin{array}{l} x \geq 0 \\ - \frac{x}{41} \geq 0 \\ x \leq (\frac{x}{41} )^2 \end{array}$ $\left\{\begin{array}{l} x \geq 0 \\ - x \geq 0 \\ x \leq (\frac{x}{41} )^2 \end{array}$ $\left\{\begin{array}{l} x \geq 0 \\ x \leq 0 \\ x \leq (\frac{x}{41} )^2 \end{array}$ Первым двум неравенствам удовлетворяет единственное число - 0. Легко заметить, что оно же удовлетворяет и третьему неравенству. Значит и исходному характеристическому свойству множества удовлетворяет одно число - число 0. $\{x\ |\ x \leq 2\sqrt{x-1} \}$ $x \leq 2\sqrt{x-1}$ $\frac{x}{2} \leq \sqrt{x-1}$ $\sqrt{x-1} \geq \frac{x}{2}$ $\left[\begin{array}{l} \left\{\begin{array}{l} x-1 \geq 0 \\ \frac{x}{2}\ \textless \ 0 \end{array} \\ \left\{\begin{array}{l} x-1 \geq 0 \\ \frac{x}{2} \geq 0 \\ x-1 \geq ( \frac{x}{2} )^2 \end{array} \end{array}$ $\left[\begin{array}{l} \left\{\begin{array}{l} x \geq 1 \\ x\ \textless \ 0 \end{array} \\ \left\{\begin{array}{l} x \geq 1 \\ x \geq 0 \\ x-1 \geq \frac{x^2}{4} \end{array} \end{array}$ Первая система не имеет решений, поэтому далее рассматриваем только вторую систему: $\left\{\begin{array}{l} x \geq 1 \\ x \geq 0 \\ x-1 \geq \frac{x^2}{4} \end{array}$ $\left\{\begin{array}{l} x \geq 1 \\ 4x-4 \geq x^2 \end{array}$ $\left\{\begin{array}{l} x \geq 1 \\ x^2-4x+4 \leq 0 \end{array}$ $\left\{\begin{array}{l} x \geq 1 \\ (x-2)^2 \leq 0 \end{array}$ Для второго неравенства получаем x=2, при этом значении х левая часть равна нулю, при других значениях х квадрат числа будет положительным. Число 2 также удовлетворяет первому неравенству. Значит исходное множество содержит один элемент - число 2.
- Автор:
  goldilocks
- 5 лет назад
- 0
$41 \sqrt{x} \leq -x$ $\left \{ {{ 0\leq 41^2x \leq (-x)^2} \atop {-x \geq 0}} ight. ; \left \{ {{ 0\leq 41^2x \leq x^2} \atop {x \leq 0}} ight. ; \left \{ {{ 41^2x \leq x^2} \atop {41^2x \geq 0}} \atop{x \leq 0} ight. ; \left \{ {{ 41^2x \leq x^2} \atop {x \geq 0}} \atop{x \leq 0} ight.$ Одновременным решением третьего и второго неравенств есть лишь одно число: $0$ Подстановкой можно убедится, что оно превращает первое неравенство в правдивое числовое неравенство: $41^2*0 \leq 0^2;0 \leq 0$ Значит множество х-ов заданно единственным числом: 0-м $x \leq 2\sqrt{x-1}$ $-2\sqrt{x-1} \leq -x$ $2\sqrt{x-1} \geq x$ $\left \{ {{x \geq 0} \atop {4(x-1) \geq x^2}} ight. ,or, \left \{ {{x\ \textless \ 0} \atop {4(x-1) \geq 0}} ight.$ $\left \{ {{x \geq 0} \atop {-x^2+4x-4 \geq 0}} ight. ,or, \left \{ {{x\ \textless \ 0} \atop {x-1 \geq 0}} ight.$ $\left \{ {{x \geq 0} \atop {x^2-4x+4 \leq 0}} ight. ,or, \left \{ {{x\ \textless \ 0} \atop {x \geq 1}} ight.$ $\left \{ {{x \geq 0} \atop {(x-2)^2 \leq 0}} ight.$ Единственное значение х-са, при котором выполняется второе неравенство это $x=2$ , которое также удовлетворяет и первое неравенство.Значит множество х-ов заданно единственным числом: 2-ой
- Автор:
  leonorpigd
- 5 лет назад
- 0
Добавить свой ответ