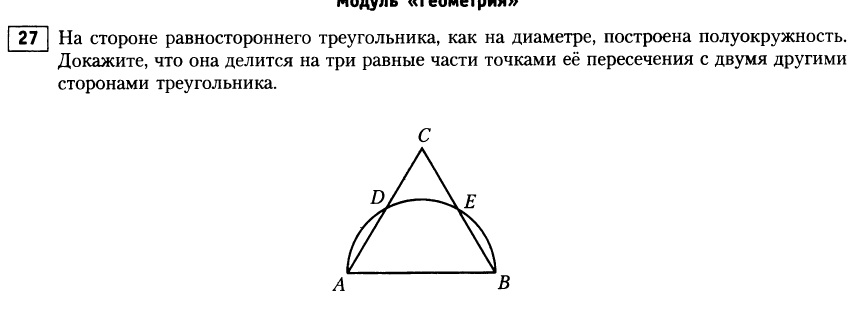
на стороне равностороннего треугольника, как на диаметре, построена полуокружность. Докажите, что она делиться на три равные части точками её пересечения с двумя другими сторонами треугольника.

 

Пусть О центр нашей окружности

Чтобы доказать, что полуокружность делится на 3 равные части нам нужно доказать, что углы АОД, ДОЕ, ЕОВ равны 

Возьмем треугольник АОД, АО=ОД так как это радиусы окружности. Угол ДАО = 60 градусов, так как треугольник АВС равносторонний, следовательно угол АДО тоже равен 60, так как треугольник АОД равнобедренный (АО=ОД), а следовательно и угол АОД тоже равен 60 градусов (180 - 60 - 60). Аналогично доказываем что угол ЕОВ = 60 градусов. Угол ДОЕ получается тоже равен 60 градусов (180 - 60 - 60). т.е. все углы равны. Что и требовалось доказать.