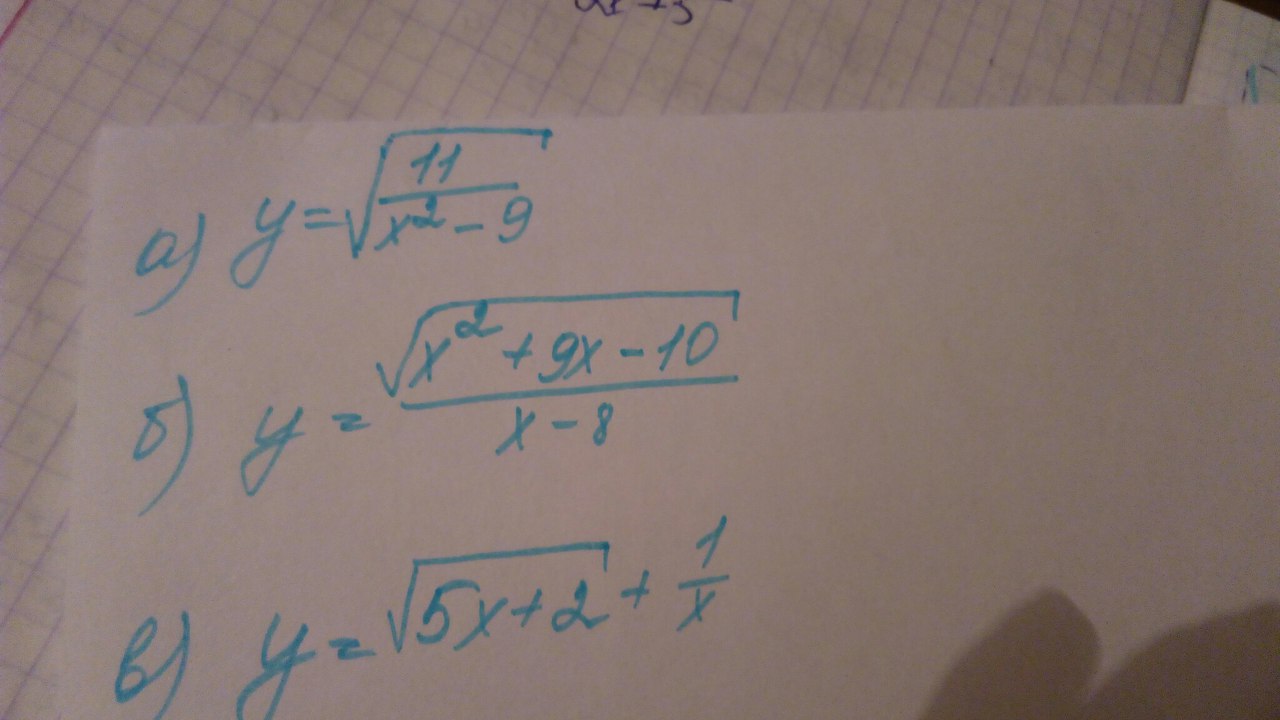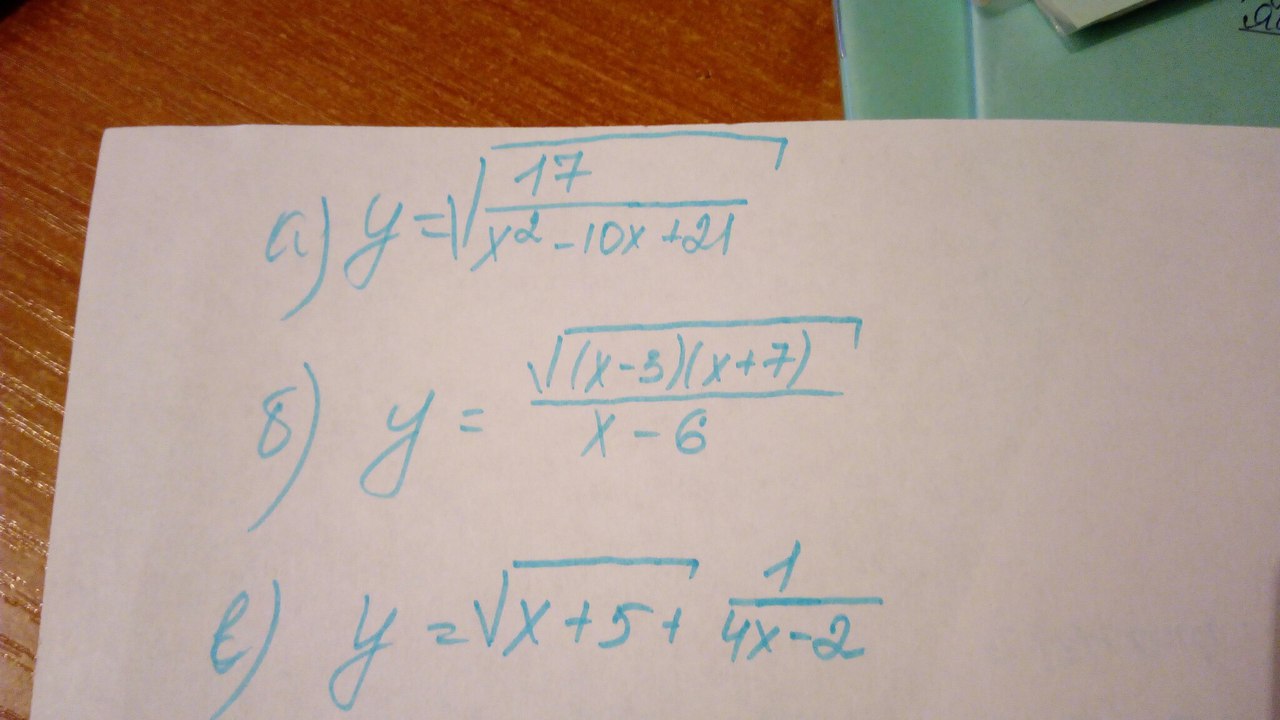Ответы 1
-
a)
ОДЗ:x²-9>0(x-3)(x+3)>0x=3 x=-3 + - +------- -3 ----------- 3 -----------\\\\\\\\\ \\\\\\\\\\\\x∈(-∞; -3)U(3; +∞)D(y)=(-∞; -3)U(3; +∞)б)
ОДЗ:1) x²+9x-10≥0 x²+9x-10=0 D=9² -4*(-10)=81+40=121=11² x₁=(-9-11)/2=-10 x₂=(-9+11)/2=1 (x+10)(x-1)≥0 + - +---------- -10 ---------- 1 -----------\\\\\\\\\\\\ \\\\\\\\\\\\\\x∈(-∞; -10]U[1; +∞)2) x-8≠0 x≠8В итоге ОДЗ: x∈(-∞; -10]U[1; 8)U(8; +∞)D(y)=(-∞; -10]U[1; 8)U(8; +∞)в)
ОДЗ:1) 5x+2≥0 5x≥ -2 x≥ -0.42) x≠0В итоге ОДЗ: x∈[-0.4; 0)U(0; +∞)D(y)=[-0.4; 0)U(0; +∞)a)
ОДЗ: x²-10x+21≥0x²-10x+21=0D=(-10)²-4*21=100-84=16=4²x₁=(10-4)/2=3x₂=(10+4)/2=7 + - +-------- 3 ---------- 7 ------------\\\\\\\\\\ \\\\\\\\\\\\\x∈(-∞; 3)U(7; +∞)D(y)=(-∞; 3)U(7; +∞)б)
ОДЗ:1) (x-3)(x+7)≥0 x=3 x= -7 + - +-------- -7 --------- 3 ----------\\\\\\\\\\ \\\\\\\\\\\\\\x∈(-∞; -7]U[3; +∞)2) x-6≠0 x≠6В итоге х∈(-∞; -7]U[3; 6)U(6; +∞)D(y)=(-∞; -7]U[3; 6)U(6; +∞)в)
ОДЗ:1) x+5≥0 x≥ -52) 4x-2≠0 4x≠2 x≠0.5В итоге ОДЗ: х∈[-5; 0.5)U(0.5; +∞)D(y)=[-5; 0.5)U(0.5; +∞)
-
Автор:
taniya - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- составить тест по биологии на тему белки жиры углеводы нуклииновые кислоты
-
1. What is that? [A — They / В — It / С — There] is my computer.
2. My brother is [A — one /B — a/C — an] officer.
3. [A — This/ В — These/С— That] flowers are very beau¬tiful.
4. Are [A — those / В — that / С — there] books interest¬ing?
5. [A — It has/В — It is/С — There is] a dog in the garden.
6. I [A — has / В — have / С — had] to go to the library tomorrow.
7. Kate is here, but her parents [A — isn't/ В — wasn't/С — aren't].
8. You ought [A — stay/В — to stay/ С — staying] at home.
9. He should [A — write/ В — to write/ С — writing] a let¬ter.
10. Mike [A — like/ В — likes/С — can] to speak English.
11. I hope you've got [A — a / В — any / С — some] money.
12. Do you want [A — know/ В — to know/C — knowing] the news?
13. We've got [A — a few/В — a little/С — a number] ap¬ples left.
14. There aren't [A — a lot/ В — many / С — much] people here today.
15. [A — Is /В — Has/ С — Does] she get up early every day?
16. Were you in Moscow last year? — No, I [A — didn't/В— weren't / С — wasn't].
17. I [A — have never been /В — was never /С — am never being] to Moscow yet.
18. [A —Isn't /B — Doesn't/С — Hasn't] she going to clean the room today?
19. The boys [A — play / В — is playing /C — are playing] football at the moment.
20. She [A — caught/В — catches /C- will catch] the 7. 30 train yesterday.
21. Kate [A — loses/В — has lost/ С — lost] her pencils very often.
22. [A — Did you do/ B — Do you do/C — Have you done] much work yesterday?
23. He [A — hurries/В —hurried/С — is hurrying] because he was late.
24. Who is she looking [A — on/В — at/С — to]?
25. Our holidays are [A — in / В — at/ С — on] August.
26. What's the matter [A — by/B — on/C — with] him?
27. This book is [A — my / В — me / С — mine].
28. Don't help him. He will do everything [A — myself/ В— himself / С — yourself]
29. We are playing [A — ours / В — our/ С — us] favourite game.
30. It is much [A — warm / В — warmer/ С — more warm] here.
31. She is not as old [A — that / B — than /C — as ] I am.
32. Ann is [A — very /В — more/С — much] intelligent than Max.
33. Yesterday was the [A — shortest/ В — most short/ С —very short] day this year.
34. We’ll listen to Professor's lecture and [A — therefore/В -then/С — than] we'll have a break.
35. He is the [A —very good/ В — best/C — better] student in the group.
36. [A— Where/B— Why/C— Who] wrote that letter?
37. She went home early [A — because/В — while/С — till] she had finished her work.
38. [A - Who/ В - Where/С- When] did you put my book?
39. [A-How/B- What/C- Where] is Bill?-Very well, thanks.
40. He drives [A — more careful / В — very carefully / С —very careful].
-
Предмет:
Английский язык -
Автор:
maverickjfxe - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
На какой слог в них падает ударение слово сантиметр,километр магазин шафёр,документ ,красивее портфель арбуз свёкла зевота дремота звонит,звонишь,баловаться ,начал,начала, начали,заперли ,заперла понял,
поняла,поняли.-
Предмет:
Русский язык -
Автор:
charlizearellano - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Кто автор высказывания с русским языком можно творить чудеса
-
Предмет:
Русский язык -
Автор:
kiannacarney - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years