Докажите, что функция: а) f(x)=x^2-2x убывает на промежутке (-∞;1].

Что и требовалось доказать!

Нужно доказать, что:

• функция f(x)={x}^{2}-2x убывает на промежутке (-\infty; \: 1]

1. Найдём производную данной функции:

f'(x)=({x}^{2}-2x)'=({x}^{2})'-(2x)'=(2\cdot{x}^{2-1})-(2\cdot1)=2x-2

2. Найдём критические (стационарные) точки:

2x-2=0 \Rightarrow 2x = 2 \Rightarrow x = 2 : 2 \Rightarrow x = 1

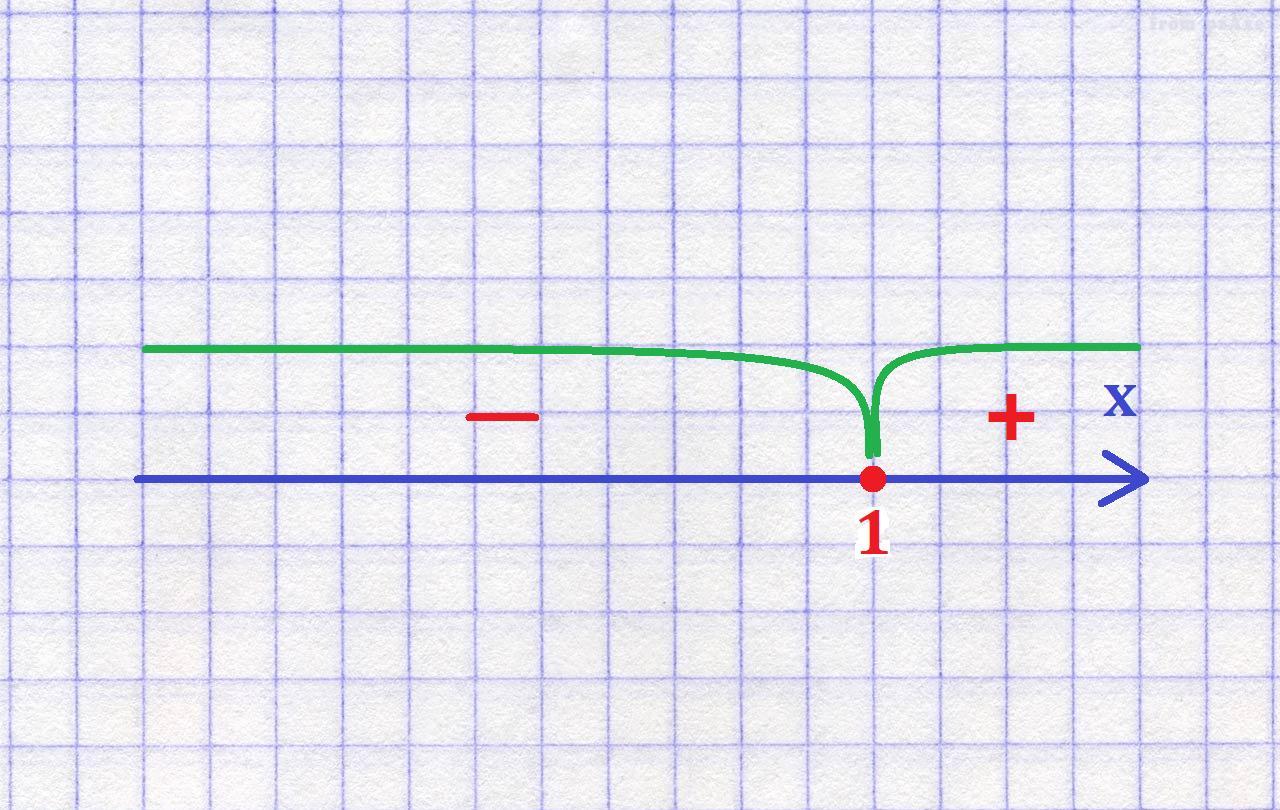
3. Исследуем критические точки на экстремум (см вложение).

--------------------------------------------------------------------------------------------------

4. Функция убывает на луче (-\infty; \: 1]. Что и требовалось доказать!