-
Помогите решить неравенство, желательно с ОДЗ и координатной прямой с отмеченными точками.
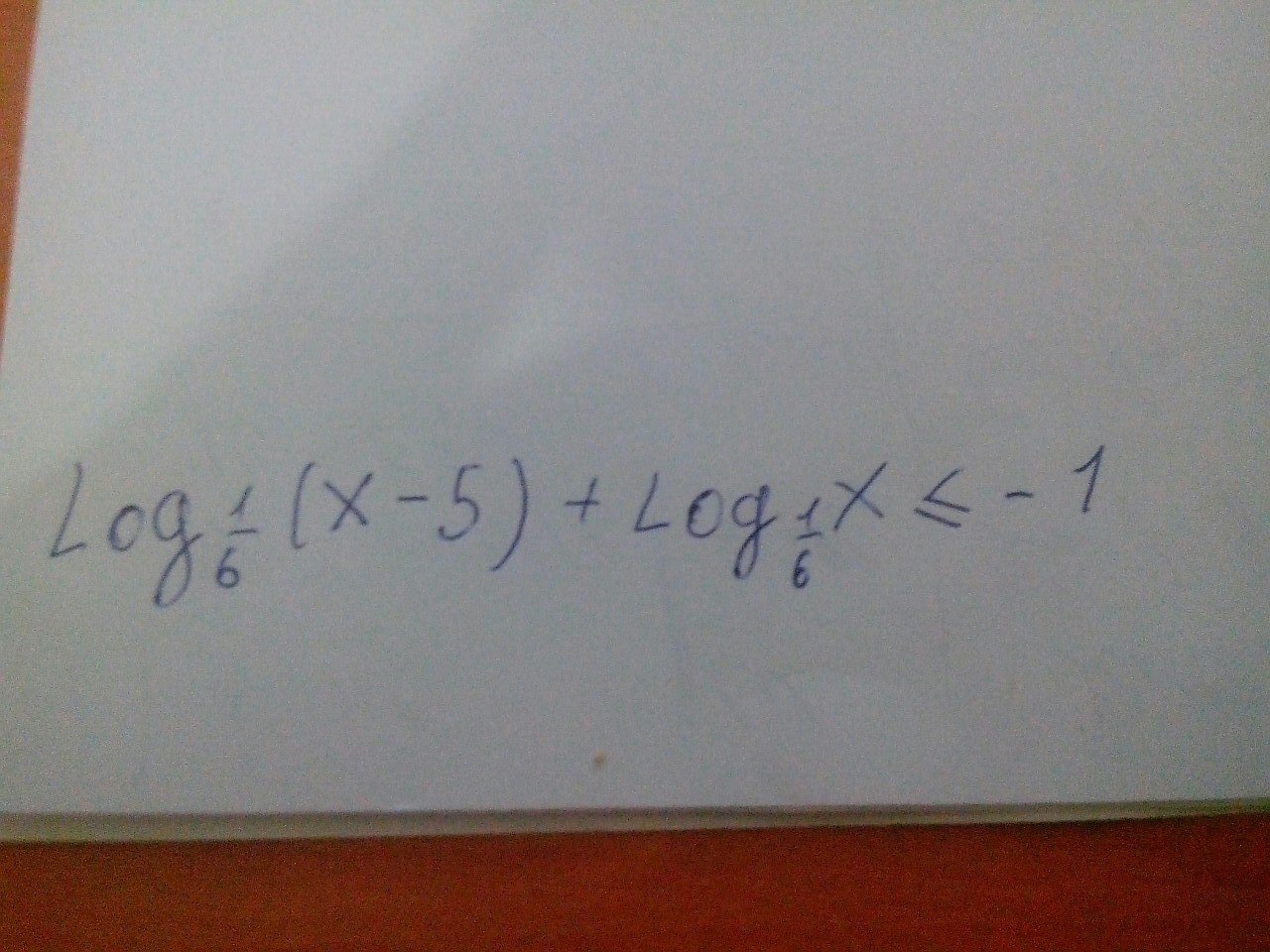
-
Предмет:
Алгебра -
Автор:
deacon26cy - 5 лет назад
-
Ответы 3
-
а само неравенство?
-
Автор:
mustachezrfj - 5 лет назад
-
0
-
-
ОДЗ
-
Автор:
moose44 - 5 лет назад
-
0
-
-
По ОДЗ
Теперь, учитывая, что нашли ОДЗ пойдём на преобразования.
Дальше решаем обычное квадратичное неравенство. Находим корни трёхчлена, методом интервалов ставим знаки и выбираем ответ, учитывая ОДЗ.
x∈(-∞;-1]∨[6;+∞), но x>5 ⇒ x∈[6;+∞)
-
Автор:
jasperrowe - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Знайдіть добуток всіх цілих чисел від -99 до 137.
-
Предмет:
Математика -
Автор:
myah - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите пожалуйста с математикой 5 класс. задание "Проведи в каждом угле биссиктрису
-
Предмет:
Математика -
Автор:
agustínhernandez - 5 лет назад
-
Ответов:
5 -
Смотреть
-
-
ПОЖАЛУЙСТА ДАЮ 62 БАЛЛА! ИЗ РЕЧИ КОРОЛЕВЫ ЕЛИЗАВЕТЫ В ТИМБЕРИ ОБРАЩЕННОЙ К АНГЛИЙСКИМ СОЛДАТАМ 1588ГОД
:Мой добрый народ те кто печётся нашей безопасности убеждали НАС ЧТО следует проявлять осторожность когда мы предстанем перед множеством вооруженных людей но Уверяю вас я не хотела бы жить не доверяю моему верному любящему народу Пусть боятся тиранЫ Я всегда жила Так что после Господа главной своей опорой и защитой считала верные сердца и доброе расположение моих подданых и посему как вы видите я сейчас среди вас не для развлеченич или забавы но полнач решимости в самой гуще и в пылу сражения остаться жить или умереть среди вас пасть во прахе во имя моего господа моего королевства моего народа моей честности и моей крови
судя по этому источнику какие чувства у английский подданых должна вызывать королевская власть
- Есть сила трения между какого нибуть напитка и какого нибуть другого напитка
How much to ban the user?
1 hour
1 day
100 years
