-
Помогите пожалуйста! Нужно решить на множестве N уравнение:
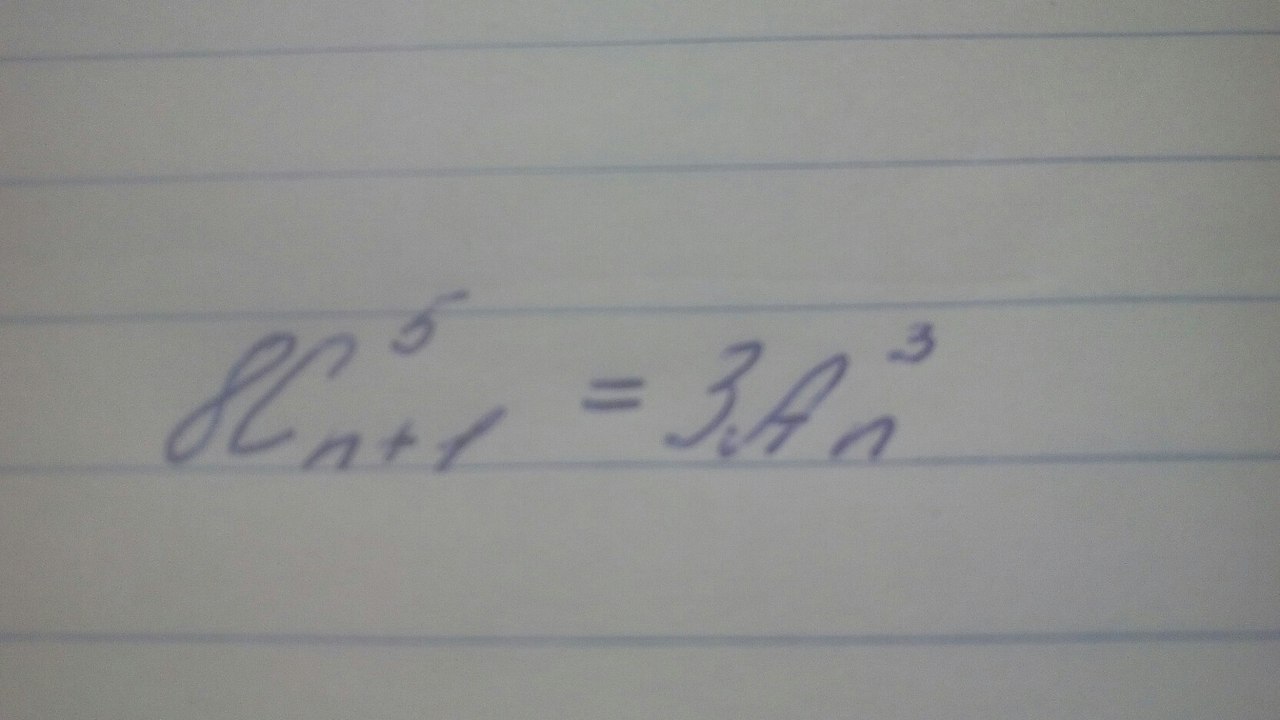
Ответы 1
-
Ответ:
-
Автор:
dum dum - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Разгадайте ребус и выберите правильное определение полученного понятия:
а) некоторый объект, способный выполнить определённый набор команд
б) последовательность команд, которые необходимо выполнить над данными для решения поставленной задачи
в) показывает количество тактов обработки данных, которые процессор производит за 1 секунду
г) это максимальная длина двоичного кода, который может обрабатываться или передаваться одновременно-
Предмет:
Информатика -
Автор:
rumplestiltskinfns2 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Какие приемы использует поэт,рисую зимнее утро?С одной стороны,пейзаж за окном,с друго-тепло и уют домашней обстановки.СРОЧНО ПЖ
-
Предмет:
Литература -
Автор:
caderhodes - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
справедливо ли сегодня в арабское изречение « Красота человека-в красоте его письма» ? объясните свою точку зрения.
-
Предмет:
История -
Автор:
amethystmine - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Отметьте сходство и различие во внешнем строении тела,в характерных движениях,окраске(рак и креветка.Пожалуйста помогите надо ,срочно!!!)
How much to ban the user?
1 hour
1 day
100 years
