-
пожалуйста решите рациональные неравенства, какие нибудь из них заранее спасибо
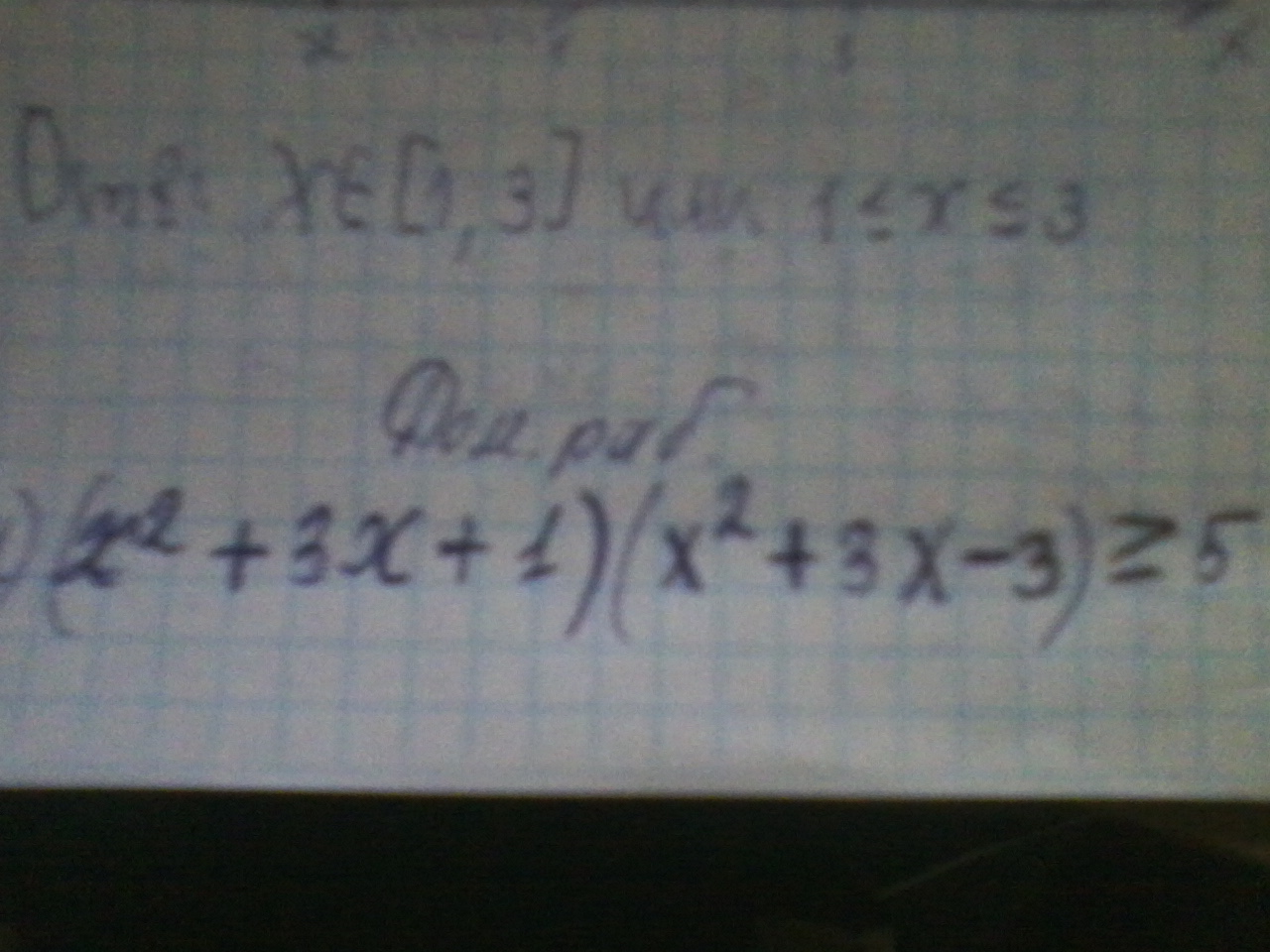
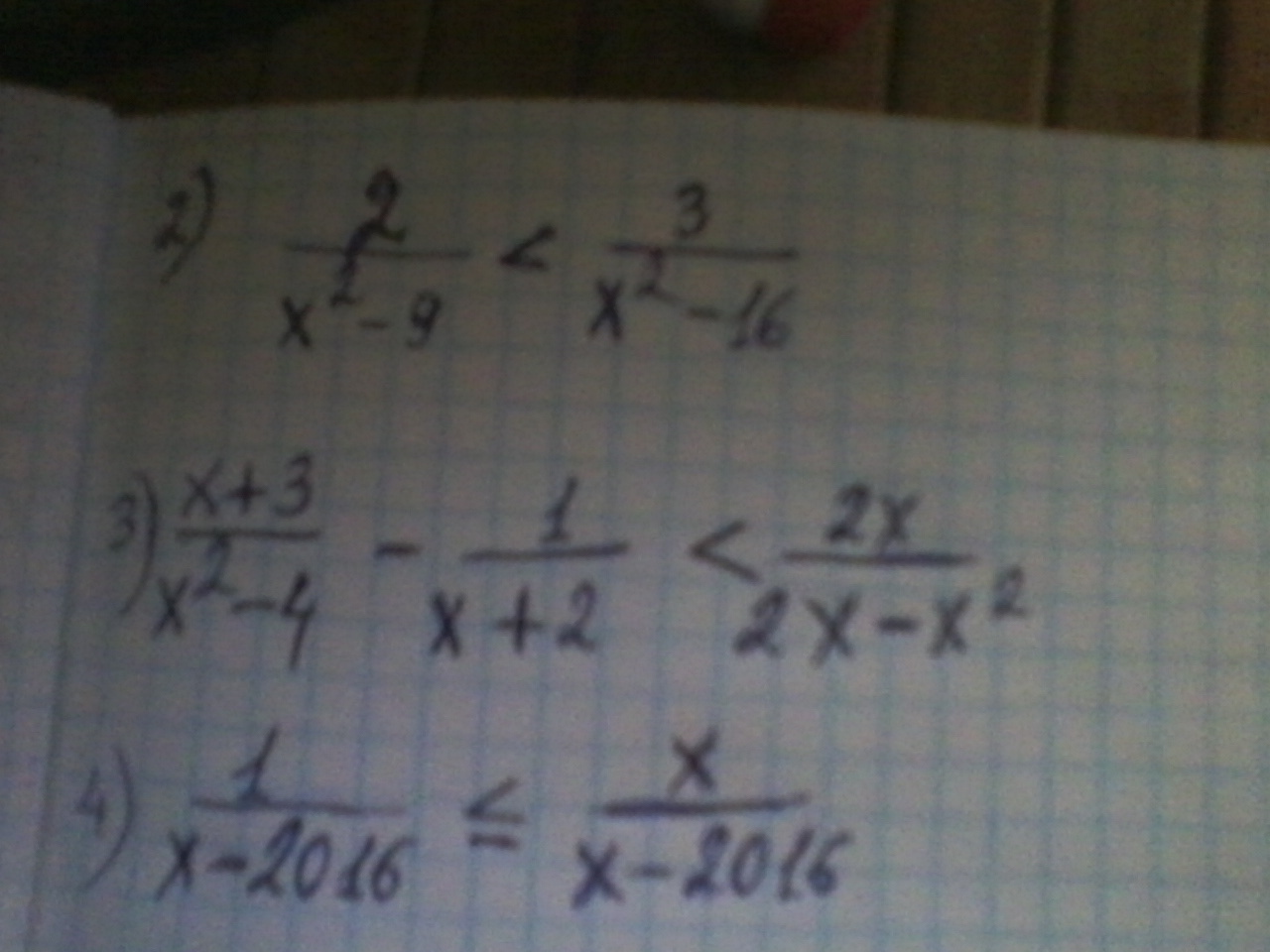
-
Предмет:
Алгебра -
Автор:
sirochristensen - 6 лет назад
-
Ответы 3
-
это неверно.
-
Автор:
buds - 6 лет назад
-
0
-
-
(x2+3x+1)(x2+3x-3)>5x2+3x+1>5x2+3x-4>0Д=9+16=25x=-3+5/2=1x=-3-5=-4x2+3x-8>0d=9+32=41x=-3+-koren41
-
Автор:
nicolasgordon - 6 лет назад
-
0
-
-
1) (х² +3х +1)(х² +3х -3) ≥ 5Обозначим: хx²+3х = t(t +1)(t -3) ≥ 5t² -2t -3 -5 ≥ 0t² -2t -8 ≥ 0 корни 4 и -2Решение этого неравенства:a) t ≤ -2 б) t ≥ 4x²+3х ≤ -2 x²+3х ≥ 4x²+3х +2 ≤ 0 x²+3х - 4 ≥ 0 корни -2 и -1 корни - 4 и 1 решение: решение:х∈ [-2;-1] х ≤ 4 и х ≥ 12)2/(х² -9) < 3/(х² -16)2/(х² -9) - 3/(х² -16)< 0(2(x² -16) -3(x² -9))/(x²-9)(x² -16) < 0(2x² -32 -3x² +27)/(x² -9(x² -16) < 0(-x² -5)/(x² -9)(x² -16)>0решаем методом интервалов)-х² -5 это число всегда с минусомх² - 9 = 0х = +- 3х² -16 = 0х = +-4-∞ -4 -3 3 4 +∞ + + - + + это знаки х² -9 + - - - + это знаки х² -16 учитываем , что есть ещё множитель отрицательный. IIIIIIIIIIIIIII IIIIIIIIIIIIIIII IIIIIIIIIIIIIIII это ответ.4)1/(х - 2016) ≤ х/(х - 2016) 1/(х - 2016) - х/(х - 2016) ≤ 0(1 - х)/(х - 2016) ≤ 0Решаем методом интервалов:нули числителя и знаменателя 1 и 2016-∞ 1 2016 +∞ - + - это знаки дробиОтвет: х∈(-∞; 1]∪(2016; +∞)
-
Автор:
haney - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Как переводится слово география
-
Предмет:
Геометрия -
Автор:
yasmingvr3 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Что такое самоотверженность и аргументы из литературы.
-
Предмет:
Литература -
Автор:
bumblebeeiway - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
в чём была сила Карлы-чародея?в сказке бой Руслана с головой
-
Предмет:
Литература -
Автор:
essencemz3e - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
объясните как 60 разделить на 15
-
Предмет:
Математика -
Автор:
michaelibcm - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
