-
Вычислите пределы функций, нужно срочно . Пожалуйста помогите кто-нибудь. Дам хороший балл.
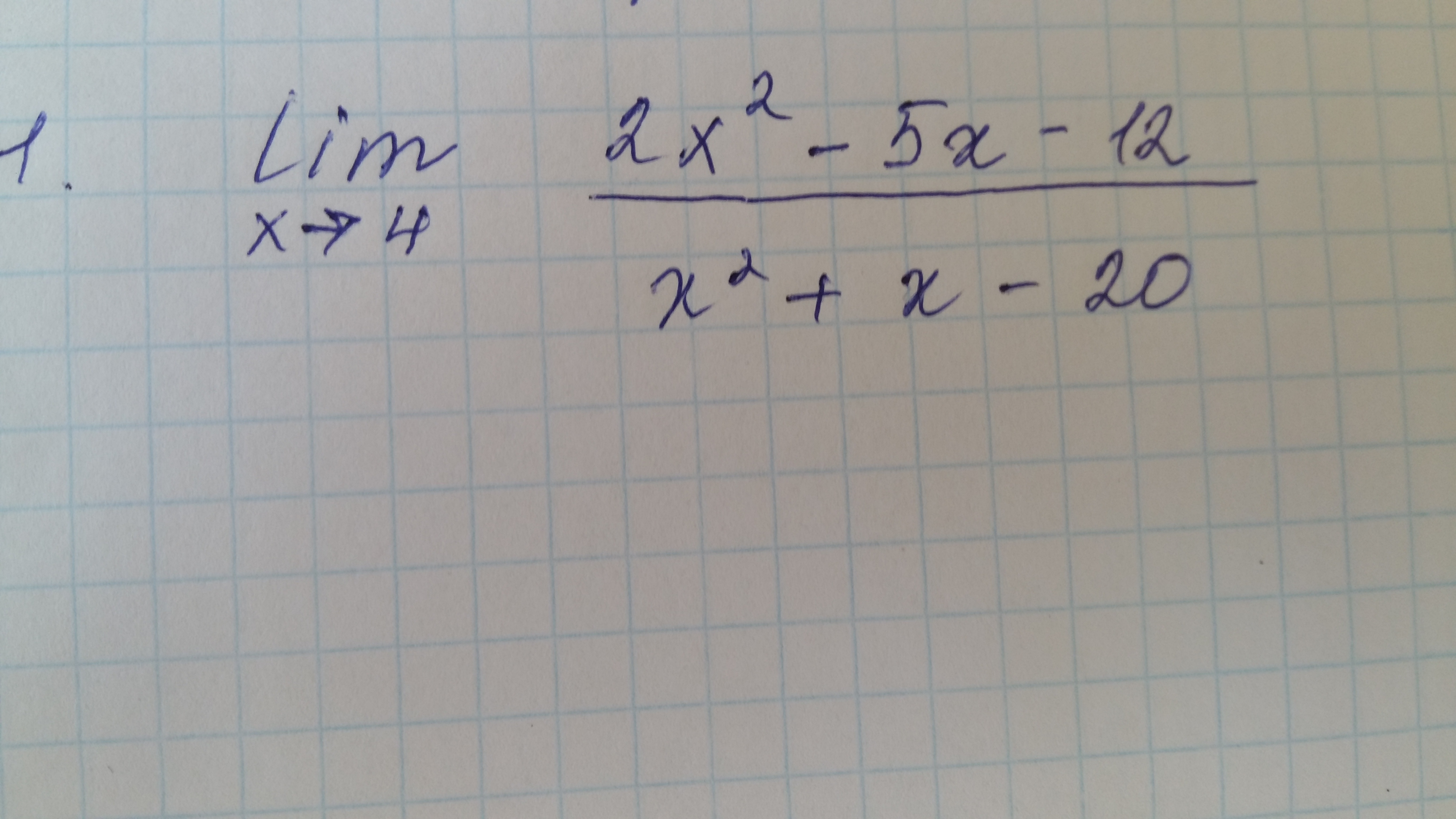
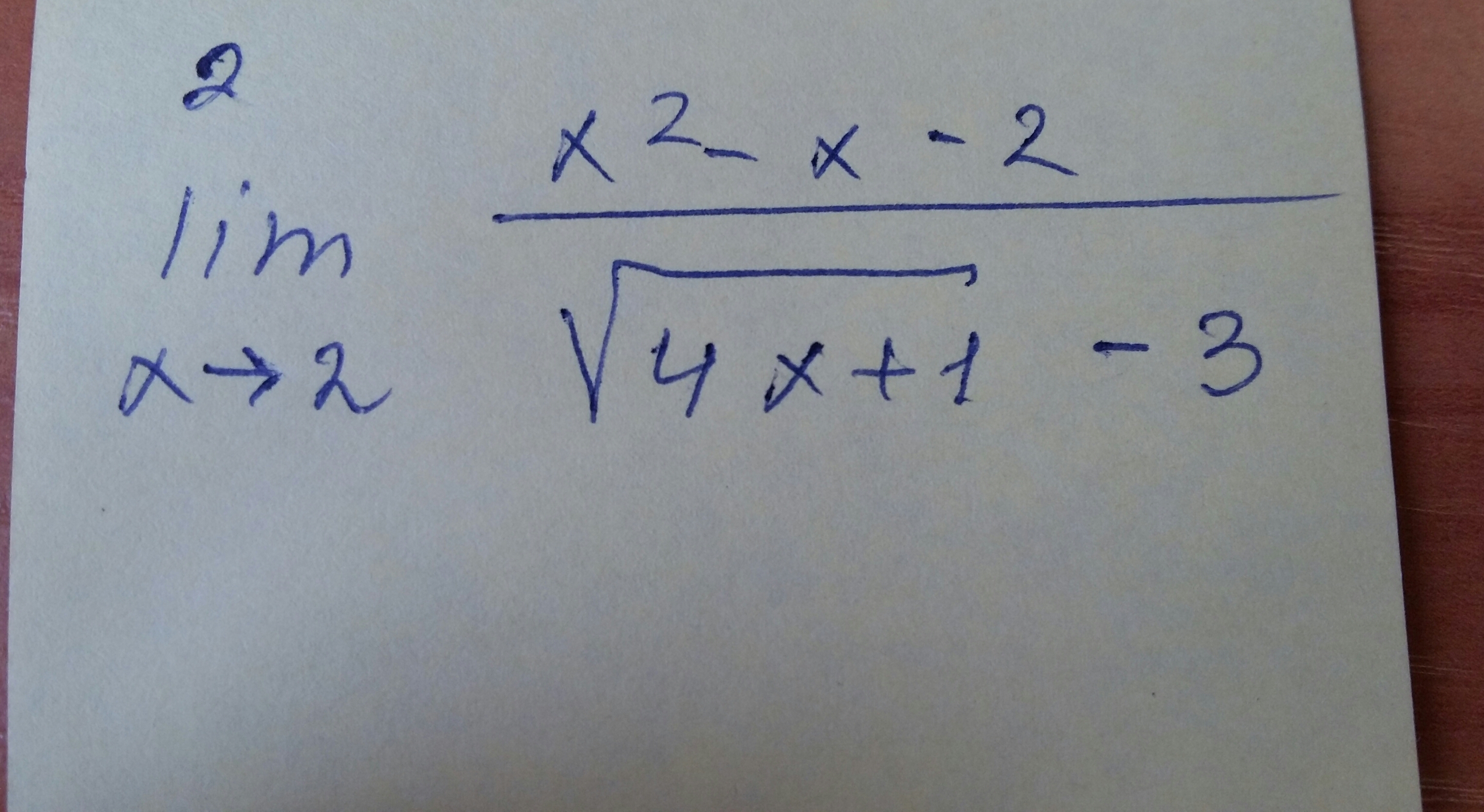
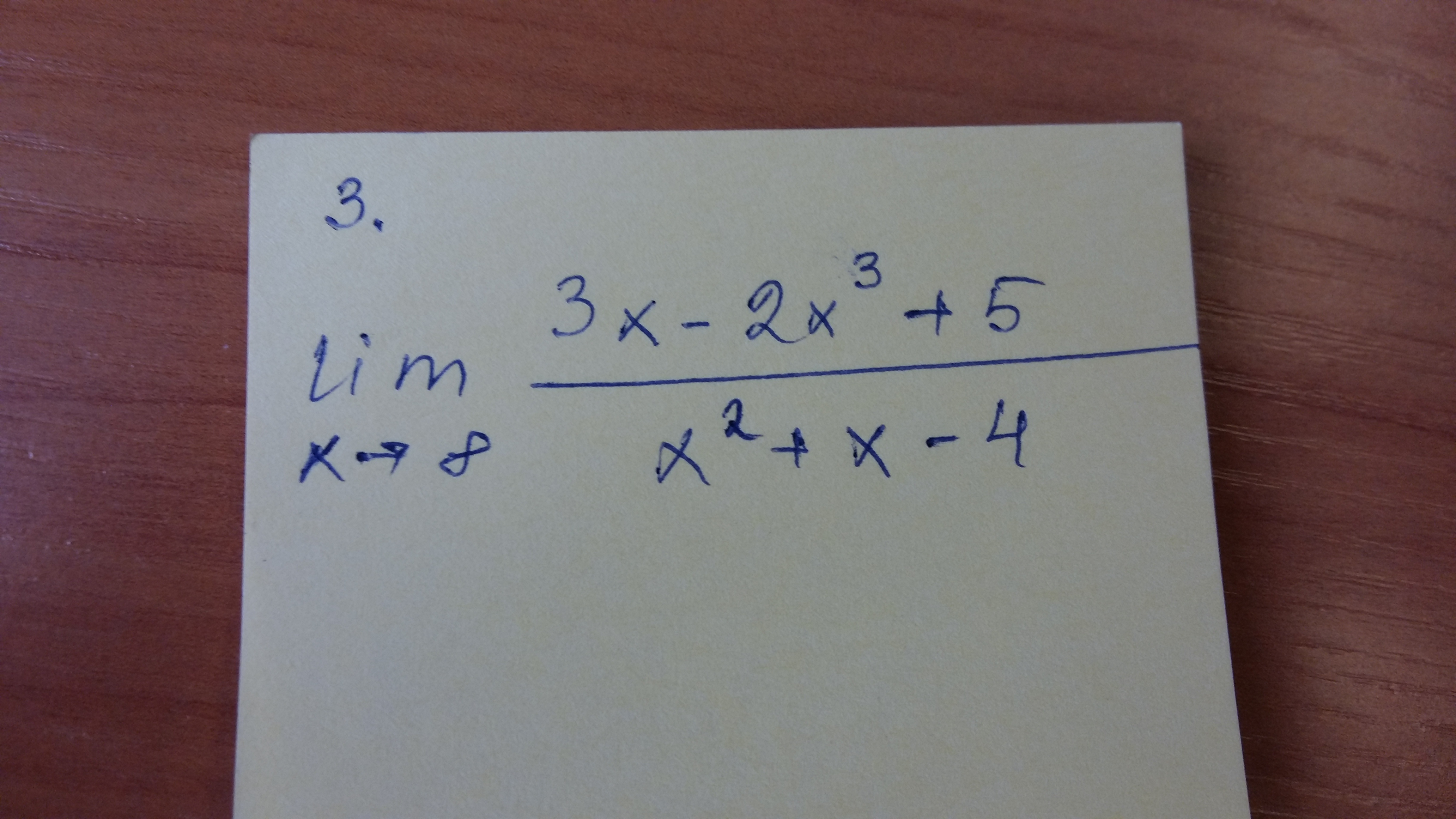
-
Предмет:
Алгебра -
Автор:
goldilocks - 6 лет назад
-
Ответы 1
-
1)
2)
3)
По правилу Лопиталя
-
Автор:
tiger9c8i - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Как решить неравенство6:х>3
-
Предмет:
Математика -
Автор:
monkey58 - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Согласны ли вы с тем что человек имеет право вмешиваться в жизнь природы?
-
Предмет:
Русский язык -
Автор:
beetlezpsv - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Переведите число 2 в десятичную систему и 10 в двоичную
-
Предмет:
Другие предметы -
Автор:
bobf9r - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
решить задачу с помощью уравнения! Луч делит развернутый угол на два угла.Найдите градусную меру этих углов,если один угол меньше другого угла в 3 раза.
-
Предмет:
Математика -
Автор:
kelley - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
