-
Помогите пожалуйста с уравнениями!!! Особенно со вторым)))
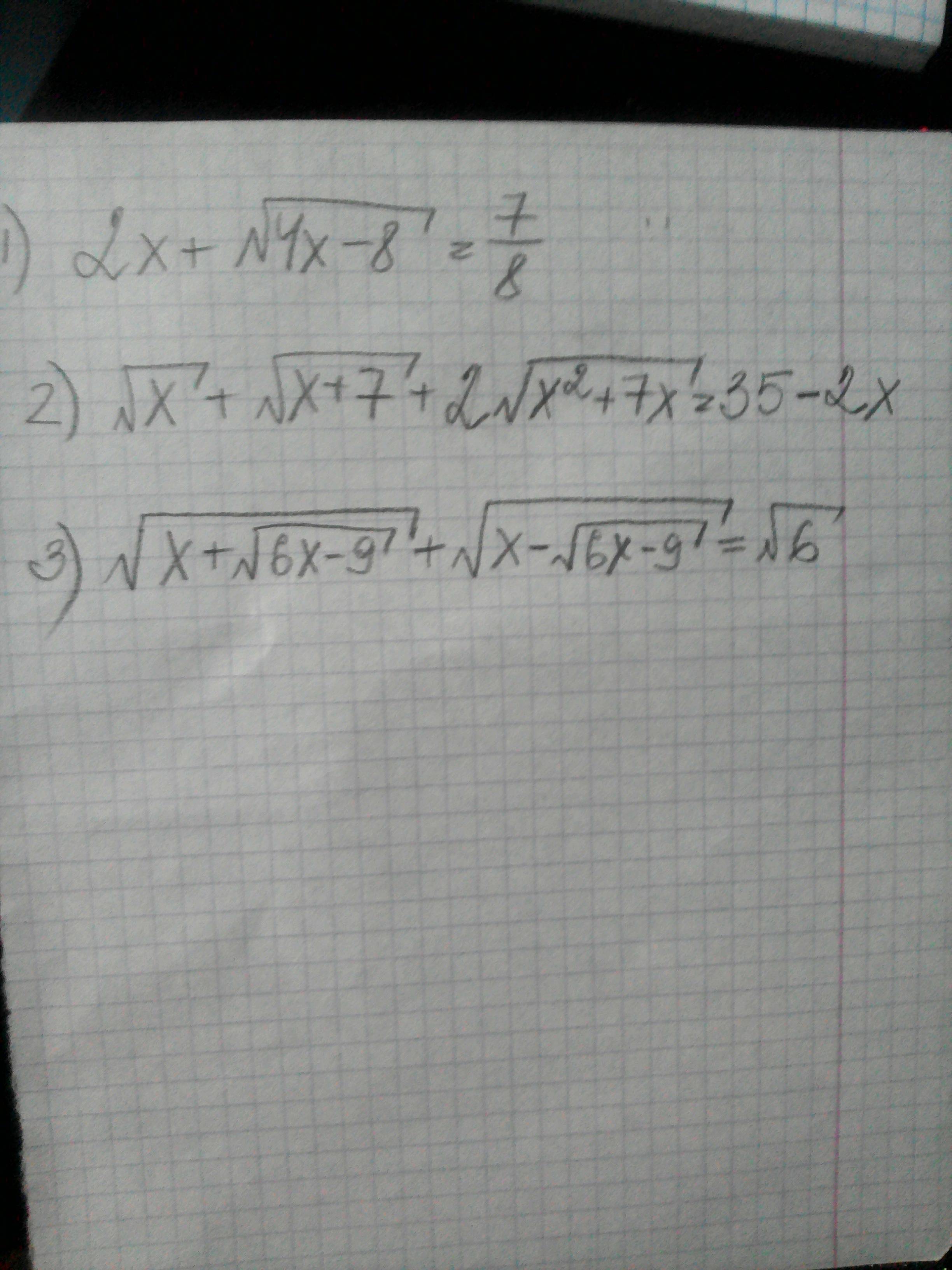
Ответы 2
-
Спасибо большое)))))))
-
Автор:
gizmottfo - 6 лет назад
-
0
-
-
1) ОДЗ: 4х-8≥0, т.е. x≥2. Тогда вся левая часть ≥4, а правая равна 7/8. Поэтому корней нет.2) Обозначим √x=a, √(x+7)=b. Заметим, что 2х=a²+b²-7. Тогда уравнение перепишется как а+b+2ab=35-(a²+b²-7)(a+b)²+(a+b)-42=0откуда a+b=6 или a+b=-7. Второе невозможно, т.к. a+b>0.Итак, √x+√(x+7)=6. √(x+7)=6-√xx+7=36-12√x+x12√x=29√x=29/12x=(29/12)²=841/144.3). Возведем обе части в квадрат:2х+2√(х²-6х+9)=6х+|x-3|=3|x-3|=3-x, откуда видно, что при х≤3 это выполнено, а при х>3 не выполнено. Осталось проверить ОДЗ: 6x-9≥0, х≥3/2. и х-√(6х-9)≥0х≥√(6х-9)х²≥6х-9(х-3)²≥0, что всегда верно.Итак, ответ: х∈[3/2;3].
-
Автор:
adalbertogarcia - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Пожалуйста!!!
Укажи все верные ответы.
Без участия бактерий производятся :
1) ячневая крупа
2) соленые огурцы
3) сыр
4) сухари -
26176:(y*56-45856)=409 умоляю помогите пол часа вожусь
-
Предмет:
Математика -
Автор:
cason6orh - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Решите уравнение. с решением уравнений . ПОМОГИТЕ ПОЖАЛУЙСТА !!! ТОЛЬКО С ДЕЙСТВИЯМИ 1.5x+12=4x+6 2.14x+8=x+47 3.45,7x-2:4=89,6-0,3x 4.4x-16=10x+2 5.3y-26+1,5y-11
- Итоги 2 мировой войны (кратко основные)
How much to ban the user?
1 hour
1 day
100 years
