Задать вопрос Регистрация
Помочь другим

  • найдите производную функции,с полным решение,пожалуйста

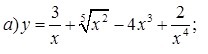
    question img

Ответы 1

  • Используя свойство:(u+v)'=u'+v'Находим:\displaystyle ( \frac{3}{x} )'=(3x^{-1})'=-3x^{-2}= -\frac{3}{x^2} \displaystyle ( \sqrt[5]{x^2} )'=(x^{ \frac{2}{5}})'= \frac{2}{5} x^{- \frac{3}{5} }= \frac{2}{5} \cdot \frac{1}{ \sqrt[5]{x^3} } = \frac{2}{5 \sqrt[5]{x^3} } (-4x^3)'=-12x^2\displaystyle ( \frac{2}{x^4} )'=(2x^{-4})'=-8x^{-5}= -\frac{8}{x^5} Теперь, следуя вышеприведенному свойству, получаем:\displaystyle f'(x)=-\frac{3}{x^2}+\frac{2}{5 \sqrt[5]{x^3} } -12x^2-\frac{8}{x^5}

    • Автор:

      dante18
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years