Задать вопрос Регистрация
Помочь другим

  • Логарифмическое неравенство
    Заранее огромное спасибо за помощь!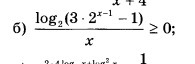

    question img

Ответы 2

  • Боже мой, спасибо ВАМ ОГРОМНОЕ! Тысячу раз спасибо!

    • Автор:

      gretawolf
    • 6 лет назад
    • 0
  • Найдем область определения дроби в левой части. Знаменатель определен при xeq 0, числитель определен, если 3\cdot 2^{x-1}-1> 0 \\ 3\cdot 2^{x-1}> 1 \\ 2^{x-1} > \frac{1}{3} \\ x-1 > log_2(\frac{1}{3}) \\ x > log_2(\frac{1}{3})+1Заметим, что log_2(\frac{1}{3})+1=-log_2(3)+1<0Таким образом, область определения дроби (log_2(\frac{1}{3})+1;0)\cup(0;+\infty)Найдем значения аргумента, при которых числитель неотрицателен:log_2(3\cdot 2^{x-1}-1)\geq 0 \\ 3\cdot 2^{x-1}-1\geq 1 \\ 3\cdot 2^{x-1}\geq 2 \\ 2^{x-1} \geq \frac{2}{3} \\ x-1 \geq log_2(\frac{2}{3}) \\ x \geq log_2(\frac{2}{3})+1log_2(\frac{2}{3})+1=log_2(2)-log_2(3)+1=2-log_2(3)>0.Таким образом, на интервале (log_2(\frac{1}{3})+1;0) и числитель и знаменатель принимают отрицательные значения, поэтому дробь принимает положительные значения и все точки этого интервала нам подойдут.На интервале (0;log_2(\frac{2}{3})+1)) числитель принимает отрицательные значения, а знаменатель принимает положительные значения, поэтому дробь принимает отрицательные значения.На луче [log_2(\frac{2}{3})+1;+\infty) числитель принимает неотрицательные значения, знаменатель принимает положительные значения, поэтому дробь принимает неотрицательные значения и все точки этого луча нам подойдут.Ответ: (log_2(\frac{1}{3})+1;0)\cup[log_2(\frac{2}{3})+1;+\infty).

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years