-
ПОМОГИТЕ срочноо хоть что-то
а) x^2+ 2x + корень x^2+2х +8 =12
б) корень x+2 + корень 3x-2 =4
И в) на фотографии ниже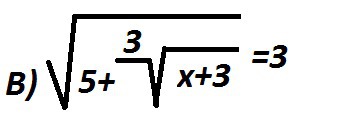
Ответы 1
-
x^2 + 2x + √(x^2 + 2x + 8) = 12; √(x^2 + 2x + 8) = t ≥ 0;x^2 + 2x + 8 = t^2; x^2 + 2x = t^2 - 8;t^2 - 8 + t - 12 = 0;t^2 + t - 20 = 0;D = 1 + 80 = 81 = 9^2 ; t1 = - 5 < 0; t2 = 4;⇒√(x^2 + 2x + 8) = 4; x^2 + 2x + 8 = 16;x^2 + 2x - 8 = 0;x1= - 4; x2 = 2.Методом подстановки проверяем оба корня, оба подходят по одз.Ответ ; х = - 4 или х = 2.2. √(x+2) + √(3x - 2) = 4;√(x+2) = 4 - √(3x - 2);x+2 = 16 - 2*4*√(3x-2) + 3x - 2;x + 2 = 14 - 8√(3x-2) + 3x;8√(3x-2)= 2x + 12;8√(3x-2) = 2(x+6);4√(3x-2) = x+6;16(3x-2) =x^2 + 12x + 36;x^2 + 12 x + 36 = 48 x - 32; x^2 - 36x + 68 = 0;D = 36^2 - 4*68 = 1296 - 272 = 1024 = 32^2;x1 = 34; x2= 2.Сравним с одз.{x+2 ≥0; x≥ - 2;3x - 2≥0 x ≥ 2/3; ⇒ одз x∈ [2/3; +∞).Оба корня подходят. Ответ х = 2 или х = 34.3. 5 + ∛(x+3) = 3^2;5 + ∛(x+3) = 9;∛(x+3) = 4; x+3 = 4^3;x+3 = 64;x = 61
-
Автор:
pepperhatm - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Прошу помогите эти 2 задания!!!!!!!!! Даю 12 баллов
-
Предмет:
Математика -
Автор:
peppa pigyoeh - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
масштаб 1:200000 на карте -12см сколько будет на месности
-
Предмет:
Математика -
Автор:
leviiiau - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите перевезти на украйнский язик
On birtday morning each had a job to do. Steve beat the eggs and made the toasts. Father fried them. Molly sprinkled the hot toasts with powdered sugar ahd set the table . She decorated the toasts with berres and honey. They didn' t forget about the kitchen . It was clean and tidy.
When mother came into the kitchen, they said together, "Happy birthday, dear Mum !"
Mother was so surprised !
She said, "This is so beautiful.Thank you very much."-
Предмет:
Английский язык -
Автор:
carlos290 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
До скольки округлено число 78691=78700?
-
Предмет:
Математика -
Автор:
lyric6kqp - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
