-
Найти интегралы: (полное решение) задания на изображении
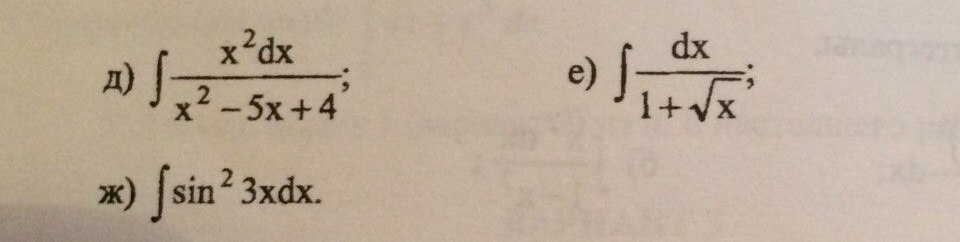
-
Предмет:
Алгебра -
Автор:
ice queenta3k - 6 лет назад
-
Ответы 1
-
-
Автор:
barbara - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
"ледники Гринландии "
-
Предмет:
География -
Автор:
foxy ladyijhf - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Что можно сказать о внутренней энергии расплавленного и нерасплавленного свинца массой 1 кг при температуре 327 градусов?
-
температура воздуха -7C.сколько градусов будет показывать термометр если:1) температура воздуха измениться на +3C, на +2? 2) температура измениться на -2, на -4 ?
-
Предмет:
Математика -
Автор:
glennbernard - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
5+5×3/4÷1 ответь и не надо писать чушь или (
я не знаю прости )если скажете
бан-
Предмет:
Математика -
Автор:
averyizq5 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
