-
Помогите с домашним заданием по алгебре 10 класс.
Нужно решить и сделать отбор корней.
Задание во вложении.
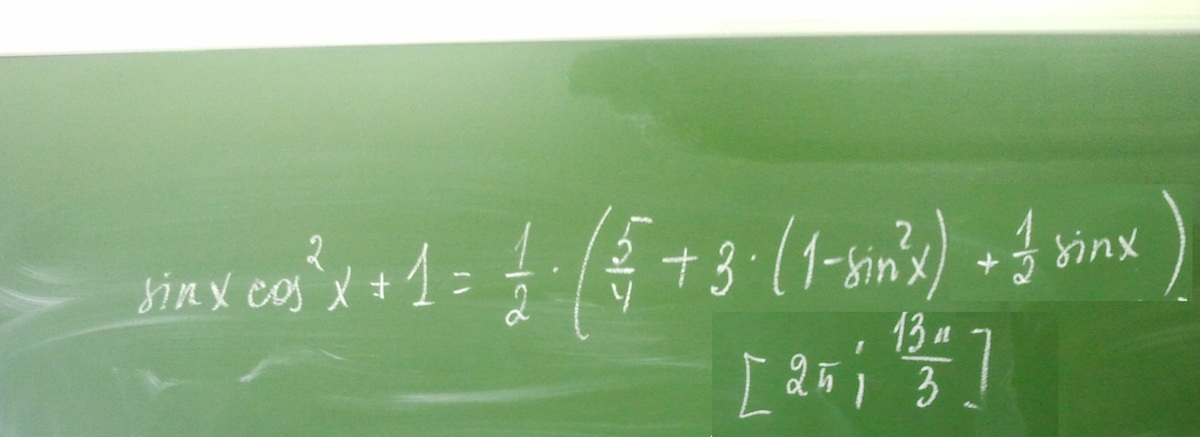
Ответы 1
-
Вторая скобка, очевидно, ни к чему хорошему не приведет. Приравниваем к нулю первую скобку:
Отбор.
1) Серия корней "+":
n=2, 7pi/3
n=3, 10pi/3
n=4, 13pi/3
2) Серия корней "-":
n=3, 8pi/3
n=4, 11pi/3
-
Автор:
penelopeynfb - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
решите неравенство
9х-11>5(2х-3)
-
Крупнейшие международные отраслевые и региональные союзы. Помогите, пожалуйста.
-
Предмет:
География -
Автор:
alvaroi8af - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Теплоход рассчитан на 980 пассажиров и 30 членов
команды. Каждая спасательная шлюпка может вместить 50
человек. Какое наименьшее число шлюпок должно быть на
теплоходе, чтобы в случае необходимости в них можно было
разместить всех пассажиров и всех членов команды?
Можно только с объяснениями? =) Просто слышала в ответе у других получилось 21 шлюпка - это как?
-
Предмет:
Математика -
Автор:
hernándezcsr0 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Вычислить объем прямоугольного параллелепипеда измерение которого равны 3,2 см, 5,7 см и 4,1 см?
-
Предмет:
Математика -
Автор:
dereonrichmond - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
