-
1) F(x)=x^5+2x^3+3x-11
[-1;1]
2) F(x)=2x+3* корень из x^2 в степени 3
[-8;1]
Найти максимум и минимум функции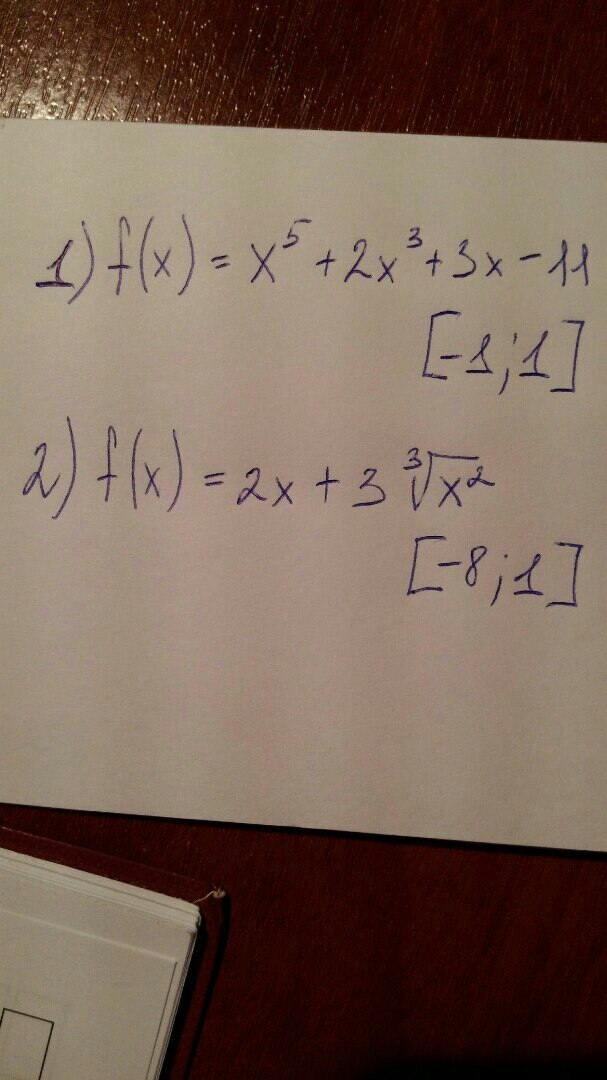
Ответы 1
-
1)F(x)=x⁵+2x³+3x-11F'(x)=5x⁴+6x²+35x⁴+6x²+3=0Пусть t=x²5t²+6t+3=0f(t)=5t²+6t+3 - парабола, ветви которой направлены вверх.D=6² - 4*5*3=36-60= -24<0Парабола не пересекает ось ОХ.Парабола лежит выше оси ОХ.Функция f(t)=5t²+6t+3 имеет только положительные значения, а значит, F'(x)=5x⁴+6x²+3 тоже имеет только положительные значения. То есть производная больше нуля, и исходная функция только возрастает - нет экстремумов.На промежутке [-1; 1]:F(-1)=(-1)⁵+2*(-1)³+3*(-1)-11=-1-2-3-11=-17 - минимальное значениеF(1)=1⁵+2*1³+3*1-11=1+2+3-11= -5 - максимальное значение.2)F(x)=2x+3*³√x²F'(x)=2+3*(²/₃)*x^(- ¹/₃)=2 + 2/x³2+2/x³ =0ОДЗ: x≠02/x³ = -2x³= -1x= -1 - экстремум функции-1∈[-8; 1]На промежутке [-8; 1]:F(-8)=2*(-8) + 3 * ³√(-8)² = -16 + 3*4= -4 - минимальное значениеF(-1)=2*(-1) + 3 * ∛(-1)² = -2 + 3=1 F(1)=2*1 + 3 * ∛1² = 2+3=5 - максимальное значение
-
Автор:
kendalldi8d - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Выполните деление и проверьте с помощью умножения 9744 :7
-
Предмет:
Математика -
Автор:
jamiya - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
какое число нужно вставить чтобы получилось верное равенство? 17 см 5 мм = ? мм , 23 м 16 см = ? см , 20026 кг = ? т ? кг, 400060 кг = ? т ? кг. 997 кг = ? ц ? кг , 9097 кг = ? т ? кг , 3000 мм ? м , 809 см = ? м 7 см .
-
Предмет:
Математика -
Автор:
chef17 - 6 лет назад
-
Ответов:
7 -
Смотреть
-
-
Изменить словосочетаниям в р.п. Купить или пушку , закрыть дверь, растопить печку, обучить молодежь, выделывать шкуру, покрасить лавку
-
Предмет:
Русский язык -
Автор:
raulvd0z - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Пожалуйста, составьте предложение из слов in/neighborhood/it's/quiet/a
-
Предмет:
Английский язык -
Автор:
judd - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
