Задать вопрос Регистрация
Помочь другим

  • ПОМОГИТЕ СРОЧНО! Даю 99 баллов за задание!!! Решите 6-7примеров на Тему “Вычисление неопределенных интегралов методом интегрирования по частям” По возможности, сфотографируйте решение и выложите картинками, буду очень признателен!

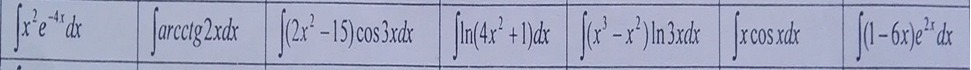
    question img

Ответы 1

  • \int\limits{x^2e^-^4^x} \, dx для решения используем метод интегрирования по частям  \int\limits{u} \, dv=uv- \int\limits{v} \, du пусть u(x)=x^2 и пусть dv(x)=e^-^4^xdx затем du(x)=2x\,dxдля того чтобы найти v(x) сделаем следующие допущения: пусть u=-4x тогда пусть du=-4dx и подставим  -\frac{du}{4} \int\limits{e^u} \, du интеграл от произведения функции на константу есть эта константа на интеграл от данной функции  \int\limits{e^u} \, du = - \frac{1}{4} \int\limits{e^u} \, du интеграл от экспоненты есть он же сам  \int\limits{e^u} \, du =e^uтаким образом результат будет - \frac{e^u}{4} проведем обратную замену переменной - \frac{1}{4}e^-^4^x при решении под-интеграла также используем интегрирование по частям по той же схеме, поэтому буду писать только сами действия без пояснений \int\limits{u} \, dv =uv- \int\limits{v} \, du \\ u(x)=- \frac{x}{2} \\ dv(x)=e^-4x\,dx \\ du(x)=- \frac{1}{2}\,dx \\ u=-4x \\ du=-4dx \\ \\ \int\limits{e^u} \, du =- \frac{1}{4} \int\limits{e^u} \, du= -\frac{1}{4} e^u \\ \\ -\frac{1}{4}e^-^4^x интеграл от произведения функции на константу есть константа на интеграл от функции \int\limits { \frac{1}{8} e^-^4^x} \, dx= \frac{1}{8} \int\limits{e^-^4^x} \, dx аналогично проведя те же манипуляции получим- \frac{1}{32}e^-^4^x в итоге получаем следующую функцию \frac{x^2}{4}e^-^4^x- \frac{x}{8}e^-^4^x- \frac{1}{32}e^-^4^x+const \\ \\ -\frac{1}{32}(8x^2+4x+1)e^-^4^x+const \int\limits ({2x^2-15)cos(3x)} \, dx \\ \int\limits {u} \, dv =uv- \int\limits {v} \, du \\ u(x)=2x^2-15 \\ dv(x)=cos(3x)\,dx \\ du(x)=4x\,dx \\ du=3\,dx \\ \\ \int\limits{cos u} \, du= \frac{1}{3} \int\limits {cos u} \, du= \frac{1}{3} sin u = \frac{1}{3}sin (3x) \\ \\ \\ u(x)= \frac{4x}{3} \\ dv(x)=sin(3x)\,dx \\ du(x)= \frac{4}{3}\,dx \\ u=3x \\ du=3dx \\ \int\limits{sin u} \, du= \frac{1}{3} \int\limits {sinu} \, du=- \frac{1}{3}cos (u) = - \frac{1}{3}cos(3x) \int\limits {- \frac{4}{9}cos (3x)} \, dx=- \frac{4}{9} \int\limits{cos 3x} \, dx \\ u=3x \\ du=3dx \\ \frac{1}{3} \int\limits{cos u} \, du= \frac{1}{3}sin (u)= \frac{1}{3}sin (3x) \\ \\ - \frac{4}{27}sin (3x) \\ \\ \\ \frac{4x}{9}cos (3x)+ \frac{1}{3}(2x^2-15)sin(3x)- \frac{4}{27}sin(3x)+const \int\limits{ln(4x^2+1)} \, dx \\ \int\limits {u} \, dv =uv- \int\limits {v} \, du \\ u(x)=ln(4x^2+1) \\ dv(x)=1 dx \\ du(x)= \frac{8x}{4x^2+1}\,dx \\ \int\limits {1} \, dx=x \\ \int\limits{ \frac{8x^2}{4x^2+1} } \, dx=8 \int\limits { \frac{x^2}{4x^2+1} } \, dx= \int\limits { \frac{1}{4}- \frac{1}{16x^2+4} } \, dx= \frac{x}{4}- \frac{1}{4} \int\limits {- \frac{1}{4x^2+1} } \, dx \\ u=2x \\ du=2dx \\ \int\limits { \frac{1}{2u^2+2} } \, du \int\limits{ \frac{1}{2u^2+2} } \, dx= \frac{1}{2} \int\limits{ \frac{1}{u^2+1} } \, dx= \frac{1}{2}arctan(u)= \frac{1}{2}arctan(2x) \\ - \frac{1}{8}arctan(2x) \\ \frac{x}{4} - \frac{1}{8}arctan(2x) \\ 2x-arctan(2x) \\ xln(4x^2+1)-2x+arctan(2x)+const  

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years