Решить предел по правилу Лопиталя. [tex] \lim_{n \to 0} (sin x)^{tgx} [/tex]Добавил фото, на

Решить предел по правилу Лопиталя.
[tex] \lim_{n \to 0} (sin x)^{tgx} [/tex]

Добавил фото, на всякий случай.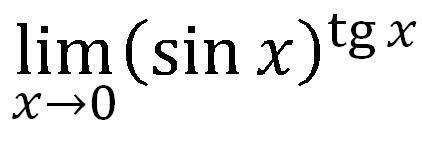
- Предмет:
  Алгебра
- Автор:
  maddie3
- 5 лет назад

Ответы 1

$lim(sinx) ^{tgx} =lime ^{(sinx) ^{tgx} } =lime ^{tgxln(sinx)} =$ $e ^{limtgx*ln(sinx)}$ Вычислим отдельно limtgx*ln(sinx)=lim[ln(sinx)/(ctgx)]=lim[(ln(sinx)]`/(ctgx)`==lim[1/sinx*cosx^(-1/cos²x]=lim(-cosx/sinx *sin²x)=lim(-sinx*cosx)=lim(-1/2*sin2x)=-1/2*0=0Нашли степень eТаким образом $lim(sinx) ^{tgx} =e^0=1$
- Автор:
  roman795
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

Кристина и Лидия одноклассники. На уроке физкультуры все ученики выстроились в колону. За Кристиной стоит ещё 16 одноклассников, среди которых и Лидия. Перед Лидией стоят ещё 14 учеников среди которых крестины . Между Лидией и Кристиной в колоне стоят 7 учеников сколько учеников в классе?
- Предмет:
  Математика
- Автор:
  sadielxdw
- 5 лет назад
- Ответов:
  
  1
- Смотреть
Прошу помочь сделать мультитест по химии.

1. Название соединения "плюмбит" образовано от названия химического элемента:
А) платина
Б) свинец
В) полоний
Г) олово

2. Электроотрицательность элементов в ряду As-P-N-O:
А) увеличивается
Б) уменьшается
В) не изменяется
Г) не определяется

3. По пять электронов на внешнем электронном уровне находится в атомах каждого из двух химических элементов:
А) рубидий и стронций
Б) азот и мышьяк
В) фосфор и кремний
Г) бром и йод

4. Укажите химический аналог с большим значением электроотрицательности для элемента сера (S):
А) селен
Б) кислород
В) фосфор
Г) хлор

5. Сколько электронов может находится на одной орбитали?
А) 0
Б) 2
В) 3
Г) 1

6. Последний электрон заполняет р-подуровень у атома элемента:
А) фосфор
Б) натрий
В) титан
Г) никель

7. К сложным веществам относится каждое из двух веществ:
А) графит и красный фосфор
Б) озон и гидроксид лития
В) аммиак и нитрат аммония
Г) йод и поташ

8. Электронная формула валентных подуровней 3s2 (двойка маленькая и находится наверху) 3p6 (с шестёркой то же самое, что и с двойкой) отвечает аниону:
А) Р3- (маленькая три минус наверху, как и в последующих)
Б) С2-
В) N3-
Г) Se2-

9. В ряду элементов P-Si-Al-Mg размеры (радиусы) атомов:
А) уменьшаются
Б) увеличиваются
В) не определяются
Г) не изменяются.
- Предмет:
  Химия
- Автор:
  biggiehkh4
- 5 лет назад
- Ответов:
  
  1
- Смотреть
каковы были последствия столетней войны для Англии?Франции?
- Предмет:
  История
- Автор:
  carloboa
- 5 лет назад
- Ответов:
  
  1
- Смотреть
СКЛАСТЫ РЕЧЕННЯ З СЛИВ ВИРНИСТЬю СОВИСТЬ, ПОДОРОЖ
- Предмет:
  Українська мова
- Автор:
  jazminberry
- 5 лет назад
- Ответов:
  
  1
- Смотреть

Решить предел по правилу Лопиталя. [tex] \lim_{n \to 0} (sin x)^{tgx} [/tex]Добавил фото, на всякий случай.

Ответы 1

Топ пользователей

Решить предел по правилу Лопиталя.
[tex] \lim_{n \to 0} (sin x)^{tgx} [/tex]

Добавил фото, на всякий случай.