-
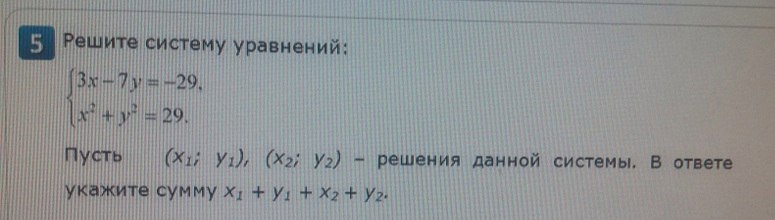
Помогите пожалуйста!!!Задание ниже)Заранее буду благодарен)))

Ответы 1
-
2x⁴+3x³-8x²-12x=0x(2x³+3x²-8x-12)=02x³+3x²-8x-12=0Свободным членом уравнения -12. Его делителями являются 1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 12; -12.Подставляем их по очереди в исходное равенство до получения тождества. При х=2 имеем2*2³+3*2²-8*2-12=0. То есть х=2 является корнем уравнения.Разделим многочлен 2x³+3x²-8x-12 на (х-2) столбиком2x³+3x²-8x-12 | x-2 ------------2x³-4x² | 2x²+7x+6---------- 7x²-8x 7x²-14x ---------- 6x-12 6x-12 -------- 0Следовательно 2x⁴+3x³-8x²-12x=x(2x³+3x²-8x-12)=x(x-2)(2x²+7x+6)Для равенства 2x²+7x+6=0, делителями будут 1; -1; 2; -2; 3; -3; 6; -6.При х=-2 получим 2(-2)²+7(-2)+6=8-14+6=0То есть х=-2 является корнем уравнения.Разделим 2x²+7x+6 на (x+2)2x²+7x+6 | x+2 -------------2x²+4x 2x+3--------- 3x+6 3x+6 ------- 0Таким образом 2x⁴+3x³-8x²-12x=x(x-2)(x+2)(2x+3)=0x=0 x-2=0 x+2=0 2x+3=0 x=2 x=-2 2x=-3 x=-3/2Ответ: 4 действительных корня уравнения.
-
Автор:
jordan905 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
(725•x-92):36=78
(912-54950:y)+483=610
Решите пожалуйста!!!-
Предмет:
Математика -
Автор:
tucker848 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
2.Основная часть.Мцыри как романтический герой.
1)прошлое героя
2)монастырь как символ неволи
3)основные черты характера юноши
а.окружающий обстановкой,картинами природы
б.в исповеди смородина
в.через эпиграф
г.через художественные стредства-
Предмет:
Литература -
Автор:
joey22 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
что такое наклонения глагола
-
Предмет:
Русский язык -
Автор:
lucianoandrade - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
раздели слова на слоги и поставь ударение яна письмо шапка радость река
-
Предмет:
Русский язык -
Автор:
talon - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
