-
ПОМОГИТЕ НАЙТИ ПРОИЗВОДНУЮ ПОЖАЛУЙСТА
ПРОШУ
с меня много баллов и лучший ответ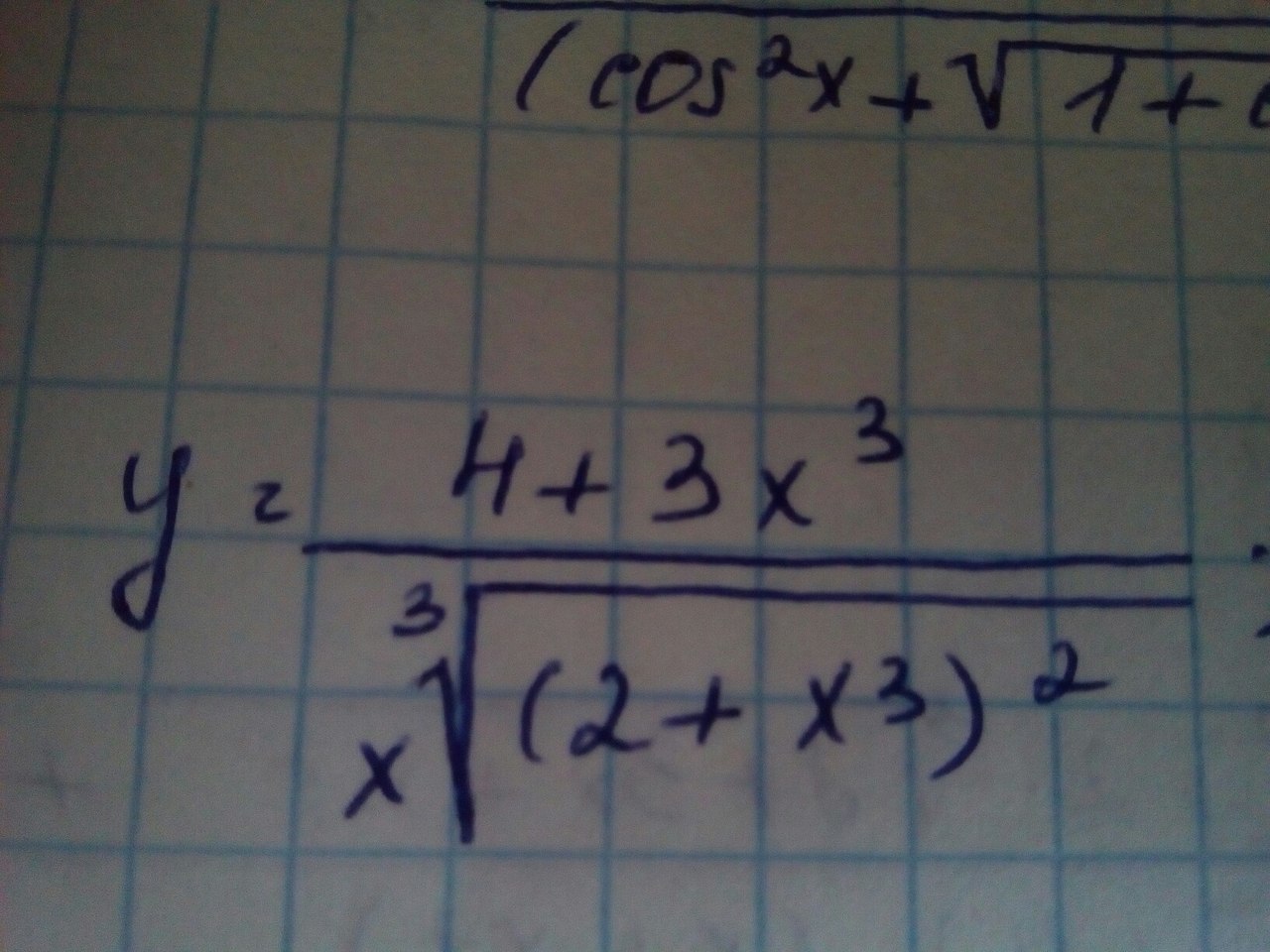
-
Предмет:
Алгебра -
Автор:
fabiánjtpe - 6 лет назад
-
Ответы 2
Еще вопросы
- алгебру 8 класса совсем не понемаю
-
Гы. Составить проект на тему "я и мой класс"
-
Предмет:
Русский язык -
Автор:
vivianzzwk - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Сколько дней в 1 недели феврале 4 недели сколько это дней
скажите какой будет ответ-
Предмет:
Математика -
Автор:
phantom6 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Каковы особенности рек в Казахстане ?Почему густота речной сети в стране разная ?
How much to ban the user?
1 hour
1 day
100 years
