-
АЛГЕБРА 11 КЛАСС. НАЙТИ ПРОМЕЖУТКИ ВОЗР. И УБЫВ. И НАИБОЛЬШИЕ, НАИМЕНЬШИЕ ЗНАЧЕНИЯ ФУНКЦИИ. СМ. ВЛОЖЕНИЕ!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
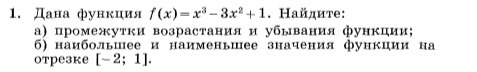
-
Предмет:
Алгебра -
Автор:
brennenwalter - 6 лет назад
-
Ответы 1
-
Дана функция
Производная равна:
Приравняем её нулю:3х²-6х = 0,3х(х-2) = 0.Отсюда получаем 2 критические точки: х = 0 и х = 2.Находим значение производной вблизи критических точек.х = -1 f' = 3*(-1)²-6*(-1) = 3+6 = 9.x = 1 f' = 3*1²-6*1 = 3-6 = -3.x = 3 f' = 3*3²-6*3 = 27-18 = 9.Этим определяются 3 промежутка знакопостоянства.Где производная больше нуля - функция возрастает:(-∞;0)∪(2;+∞),где производная меньше нуля - функция убывает: (0;2).Минимум и максимум функции также находим из свойства производной :где производная меняет знак с + на - там максимум (это точка (0;1), где производная меняет знак с - на + там минимум функции (точка(2;-3).
-
Автор:
maryperry - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
завершите предложения. Вставив правильный ответ.
Хроническое воспаление миндалин-.........................
В своей верхней части желудок заполнен...........................
Вырост слепой кишки.............................
В толстом кишечнике в кровь высасываются.........................
Пищеварение происходит под действием....................................., которое вырабатывают............................................................
очень срочно!!! Заранее спасибо)))-
Предмет:
Биология -
Автор:
rykercampos - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Люди, помогите пожалуйста!!!!!!!!! Даю ВСЕ СВОИ БАЛЛЫ!!!! ОЧЕНЬ СРОЧНО!!!!!!!!!!
Нужно исправить предложения:
1) The Tower of London is the official residence of Queen Elisabeth II
2) There are more than 20 parks in and around London which are crowned by the Crown.
3) London Zoo is situated in St. James Park
4) King Henry VIII had eight wifes
5) King Henry VIII became head of the Roman Catholic Church in 1534
6) Queen Victoria ruled England in the 16th century.
7) The Royal Albert Hall has rich collections of paintings and other works of art.
8) During the reign of Queen Elizabeth I Britain became an empire with a lot of colonies
9) Queen Elizabeth I ruled for the longest period of English story.-
Предмет:
Английский язык -
Автор:
buckeye - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Merry Christmas Twitter, Enjoy the Time with your lovely ones
Перевести точно. Начало что-то "С рождеством Твиttер, ... ?
Не гyгл переводчик с:-
Предмет:
Английский язык -
Автор:
abramclayton - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В прямоугольном треугольнике АВС А=900, AВ = 12 см, . Найдите СВ и АС. пожалуйста
-
Предмет:
Геометрия -
Автор:
vivianamccormick - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
