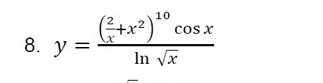Ответы 2
-
Спасибо)
-
Автор:
kassidynxp3 - 6 лет назад
-
0
-
-
(2/x+x²)¹⁰ cosxy=--------------------- обозначим функции в числителе и знамeнателе u;v ln √x(u/v)'=1/v²[u'v-v'u] для нахождения u' используем обозначение rt u=rt(rt)'=r't+t'r=[(2/x+x²)¹⁰]'cosx-(2/x+x²)¹⁰ sinx=10(2/x+x²)⁹* (-2/x²+2x)cosx-- (2/x+x²)¹⁰ sinx =Av=ln√xv'=1/√x *1/2√x=1/2xy'=(u/v)'=(1/ln²√x)[A*ln√x-(2/x+x²)¹⁰*cosx (1/2x)]
-
Автор:
blackburn - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
ИСТОРИЯ
ВОСТОЧНЫЕ СЛАВЯНЕ В РАННЕМ СРЕДНЕВЕКОВЬЕ
ПОЖАЛУЙСТА ! -
посреди стены дома длиной 20 м,ширина которого 10 м,находится электрическая розетка.Шнур длинной 18м соединяет электропроводку.Наибольшая площадь газона которую можно исключить этой персидской,приближенного равна...(выберите наиболее точное значение А492.Б442.В392.Г342)
-
Предмет:
Математика -
Автор:
pandorabradshaw - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
если к 19 прибавить задуманное мною число,то получится 37.Какое число я задумал?
-
Предмет:
Математика -
Автор:
cristianwells - 6 лет назад
-
Ответов:
4 -
Смотреть
-
- Apricis leo sub sidera, помогите перевести с латыни на русский.
How much to ban the user?
1 hour
1 day
100 years