-
Всем доброго времени суток! :)
Не могу никак решить это выражение, помогите пожалуйста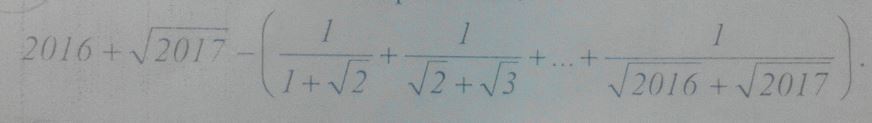
-
Предмет:
Алгебра -
Автор:
harrymaxwell - 6 лет назад
-
Ответы 1
-
Идея проста:
Теперь ясно что в большой скобке сократится все кроме √(2017)-1Тогда значение выражения равно 2016+√(2017)-(√(2017)-1)=2017
-
Автор:
missiebarron - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
решите уравнение пожалуйста
х^2+6=5-
Предмет:
Математика -
Автор:
kassandra - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
жана создер казак тыли комектесындерш
-
Предмет:
Қазақ тiлi -
Автор:
sophia65 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Найди закономерность чисел 1,02 2,04 4,07 8,11 16,16
-
Предмет:
Математика -
Автор:
cisco - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
В гости к пословицам. Прочитай. Найди глаголы в неопределенной форме.
1. Лучше хорошо поступать,чем хорошо говорить. 2. Под землей зерну не улежать. 3. Не стыдно нк знать, стыдно но не учиться. 4. Повторять да учить - ум точить. 5. Люби не только брать,но и отдавать-
Предмет:
Русский язык -
Автор:
stephanywaller - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
