-
8 класс. Решите уравнение (1)
Тема "уравнения, приводящиеся к квадратным уравнением".
Спасибо. ^-^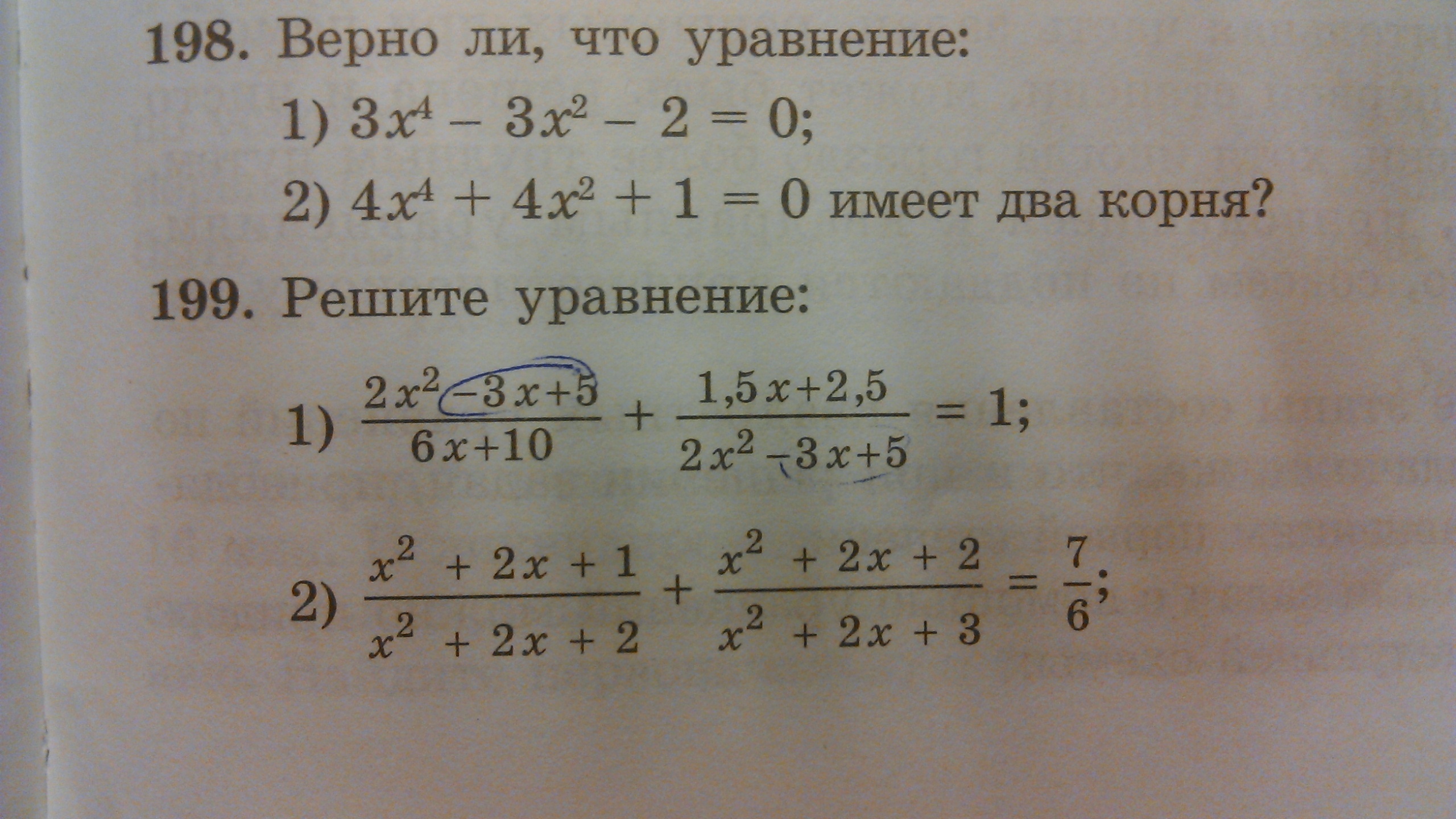
Ответы 1
-
198. Это биквадратные уравнения.1) 3x^4 - 3x^2 - 2 = 0Замена y = x^2 >= 0 при любом x.3y^2 - 3y - 2 = 0D = 3^2 - 4*3(-2) = 9 + 24 = 33y1 = (3 - √33)/6 < 0 - не подходитy2 = (3 + √33)/6 > 0 - подходит.x1 = -√(y2) = -√[(3 + √33)/6]x2 = √(y2) = √[(3 + √33)/6]Да, оно имеет 2 корня.2) 4x^4 + 4x^2 + 1 = 0Замена y = x^2 >= 0 при любом x.4y^2 + 4y + 1 = 0(2y + 1)^2 = 0y1 = y2 = -1/2 < 0 - не подходит.Нет, оно вообще не имеет корней.199. 1)
Замена
0,5 = 1/2, поэтому можно переписать так:
Умножаем все на 2yy^2 + 1 = 2yy^2 - 2y + 1 = 0(y - 1)^2 = 0y1 = y2 = 1.Обратная замена
2x^2 - 3x + 5 = 3x + 52x^2 - 6x = 02x(x - 3) = 0x1 = 0; x2 = 3
-
Автор:
kendrickbriggs - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
составить задачу с решением на тему решение задач на составление уравнения
-
Предмет:
Математика -
Автор:
braylonqy5f - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
даны Две окружности радиус первой окружности равен 4 сантиметров Это составляет четыре пятых радиуса второй окружности Найдите диаметр второй окружности
-
Предмет:
Математика -
Автор:
arnold90 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
ПОМОГИ РЕШИТЬ НОМЕР
5, 8, 9, ПЖ
КТО ОТВЕТИТ НА ТОГО Я ПОДПИШУСЬ
-
Предмет:
Математика -
Автор:
makenzie2onm - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
10 слов с сочетаниями ча ща
-
Предмет:
Русский язык -
Автор:
caitlynnjps - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
