Задать вопрос Регистрация
Помочь другим

  • Алгебра, 10 класс. Доказать тождество: (sin(t)) / (4cos(t/2)cos^2(t/4)) = tg(t/4)
    Это то, к чему я пришёл. Начальное уравнение во вложении.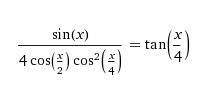

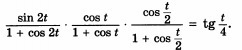
    question img
    question img

Ответы 6

  • Это всё берётся из формулы двойного угла

    • Автор:

      aprilneal
    • 5 лет назад
    • 0
  • sin(t/2)=2sin(t/4)cos(t/4)

    • Автор:

      tikibjsn
    • 5 лет назад
    • 0
  • sin2a = 2sina*cosa

    • Автор:

      moosecz5o
    • 5 лет назад
    • 0
  • также со всеми формулами можно сделать
  • sinx=2sin(x/2)cos(x/2)2sin(x/2)cos(x/2)/4cos(x/2)*cos²(x/4)=sin(x/2)/2cos²(x/4)=sin(x/2)/1+cosx/2 понизил степень 2sin(x/4)cos(x/4)/sin²(x/4)+cos²(x/4)+cos²(x/4)-sin²(x/4)=2sin(x/4)cos(x/4)/2cos²(x/4)=sin(x/4)/cos(x/4)=tg(x/4) Вроде подробно!
  • ...= \frac{\sin t }{4\cos \frac{t}{2}\cos^2\frac{t}{4}} = \frac{2\sin\frac{t}{2}\cos \frac{t}{2}}{4\cos \frac{t}{2}\cos^2\frac{t}{4}} = \frac{2\sin\frac{t}{4}\cos\frac{t}{4}}{2\cos^2\frac{t}{4}} = \frac{\sin\frac{t}{4}}{\cos\frac{t}{4}} =tg\frac{t}{4}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years