-
Помогите решить уравнения и неравенства, пожалуйста. Продам душу за решение хотя бы нескольких логов ♥
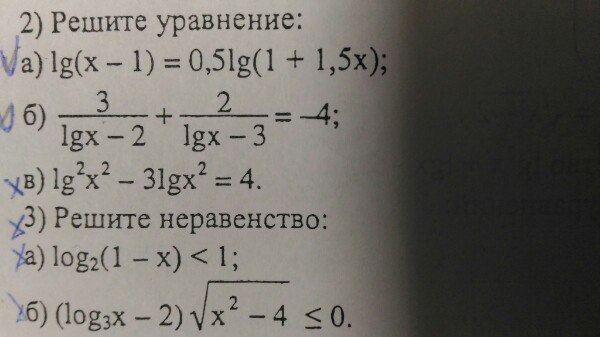
Ответы 3
-
Решил.
-
Автор:
heath80 - 5 лет назад
-
0
-
-
Удачи!
-
Автор:
snuggles34 - 5 лет назад
-
0
-
-
2.a) lg(x-1)=0,5*lg(1+1,5x) |×2 ОДЗ: x-1>0 x>1 1+1,5x>0 x>-2/3 ⇒ x∈(1;+∞)2*lg(x-1)=lg(1+1,5x)lg(x-1)²=lg(1+1,5x)(x-1)²=1+1,5xx²-2x+1=1+1,5xx²-3,5x=0x*(x-3,5)=0x₁=0 ∉ОДЗ x=3,5.б) 3/(lgx-2)+2/(lgx-3)=-43*lgx-9+2lgx-4=-4lg²x+4*5lgx-4*6 ОДЗ: x>05lgx-13=-4lg²x+20lgx-244lg²x-15lgx+11=0 lgx=t4t²-15t+11=0 D=49t₁=1 lgx=1 x₁=10t₂=2,75 lgx=2,75 x₂=10^(2,75).lg²x²-3*lgx²=4lgx²=tt²-3t-4=0 D=25t₁=4 lgx²=4 x²=10⁴ x₁=100 x₂=-100t₂=-1 lgx²=-1 x²=10⁻¹=0,1 x₃=√0,1 x₄=-√0,1.3.a) log₂(1-x)<1 ОДЗ: 1-x>0 x<1log₂(1-x)<log₂21-x<2x>-1 ⇒ Согласно ОДЗ:x∈(-1;1).б) (log₃x-2)*√(x²-4)≤0ОДЗ: x>0 x²-4≥0 (x+4)(x-4)≥0 -∞____+____-4____-____4____+____+∞x∈(-∞;-4]U[4;+∞) ⇒ x∈[4;+∞).Так как √(x²-4)≥0 ⇒log₃x-2≤0log₃x≤2log₃x≤log₃9x≤9 ⇒ Согласно ОДЗ:x∈[4;9].
-
Автор:
buddyrose - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
железная дорога своими словами
-
Предмет:
Литература -
Автор:
brindle - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Знайдіть периметр прямокутника зі стороною 10 см і діагоналлю 26.
-
Предмет:
Геометрия -
Автор:
yamiletnovak - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
информация об ипатьевской летописи.
_________________________________
заранее спасибо! -
1)3:1/9=?
Сколько получится???-
Предмет:
Математика -
Автор:
josiahgutierrez - 5 лет назад
-
Ответов:
5 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
