Задать вопрос Регистрация
Помочь другим

  • ПОМОГИТЕ РЕШИТЬ УРАВНЕНИЕ,ПОЖАЛУЙСТА,ОЧЕНЬ СРОЧНО

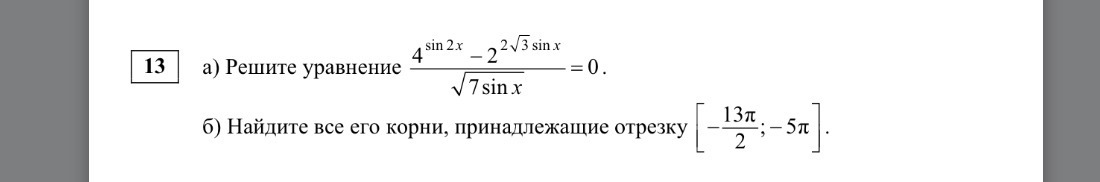
    question img

Ответы 1

  • a) ОДЗ: Знаменатель не должен равняться нулю:также подкоренное выражение должно всегда быть ≥0, так как корень квадратный стоит в знаменателе,значит подкоренное выражение должно быть строго больше нуля:7sinx\ \textgreater \ 0 \\ sinx\ \textgreater \ 0 \\ x \in (2 \pi n; \pi +2 \pi n), n \in ZРешение:Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.4^{sin2x}-2^{2 \sqrt{3} sinx}=0 \\ 2^{2sin2x}-2^{2 \sqrt{3} sinx}=0 \\ 2^{2sin2x}=2^{2 \sqrt{3} sinx} \\ 2sin2x=2 \sqrt{3} sinx \\ \\ 4sinx*cosx-2 \sqrt{3} sinx=0 \\ \\ 2sinx(2cosx- \sqrt{3} )=0 \\ \\ 1)2sinx=0 \\ sinx=0 \\ x= \pi n, n \in Z   -   не удовлетворяет ОДЗ.2) 2cosx- \sqrt{3} =0 \\ \\ cosx= \frac{ \sqrt{3} }{2} \\ \\ a) \ x= \frac{ \pi }{6}+2 \pi n, n \in Z b) \ x=-\frac{ \pi }{6}+2 \pi n, n \in Z - не удовлетворяет ОДЗOTBET: \frac{ \pi }{6}+2 \pi n, n \in Zб)  - \frac{13 \pi }{2} \leq \frac{ \pi }{6}+2 \pi n \leq -5 \pi \\ \\ - \frac{13 \pi }{2}-\frac{ \pi }{6} \leq 2 \pi n \leq -5 \pi -\frac{ \pi }{6} \\ \\ - \frac{20 \pi }{3} \leq 2 \pi n \leq - \frac{31 \pi }{6} \ |* \frac{1}{2 \pi } \\ \\ - \frac{10}{3} \leq n \leq - \frac{31}{12} \\ \\ -3 \frac{1}{3} \leq n \leq - 2\frac{7}{12} \\ \\ n=-3; \\ \\ \frac{ \pi }{6}+2 \pi n=\frac{ \pi }{6}+2 \pi *(-3)=\frac{ \pi }{6}-6 \pi =- \frac{35 \pi }{6} \\ \\ OTBET: -\frac{35 \pi }{6}

    • Автор:

      babs
    • 4 года назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years