-
Пожалуйста, решите уравнение! Не один день бьюсь над ним!
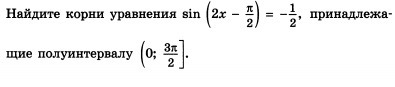
-
Предмет:
Алгебра -
Автор:
halflingnvqb - 5 лет назад
-
Ответы 2
-
здесь нужно воспользоваться двумя формулами:1) формула приведения:
2) sin(-a)=-sinaРешение:
нас интересует промежуток начиная с нуля, поэтому отрицательные корни можно отбросить. Оставляем только:
теперь вместо n подставляем числа, начиная с нуля:
π/6 входит в наш промежуток
7π/6 входит так как находится в 3-ей четверти
Не подходит, так как угол 13π/6 > 3π/2
-
Автор:
jacqueline - 5 лет назад
-
0
-
-
-
Автор:
theodorebeck - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Из объявления фирмы, проводящей обучающие семинары:
«Стоимость участия в семинаре — 3000 р. с человека. Группам от организаций предоставляются скидки: от 3 до 10 человек –– 5%; более 10 человек –– 8%».
Сколько должна заплатить организация, направившая на семинар группу из 8 человек?-
Предмет:
Алгебра -
Автор:
calixtosddr - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
1.Площадь круга через радиус.
2.Площадь круга через диаметр.
3.Длина окружности через радиус.
4.Длина окружности через диаметр.
5.Площадь прямоугольника.
Формулы.-
Предмет:
Математика -
Автор:
lillyeaim - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Як впливала сувора гірська природа на гуцулів язичників у творі " тіні забутих предків"?
(Якщо можна якійсь цитати з твору)-
Предмет:
Українська література -
Автор:
kayleek5sc - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Из магазина на хлебозавод выехала машина со скоростью 45 км/ч,одновременно с ней из хлебозавода в магазин выехала другая машина со скоростью 40км/ч Когда первая машина приехала на хлебозавод,второй оставалось проехать ещё 10км Найди растояние между магозином и хлебозаводом.
-
Предмет:
Математика -
Автор:
arnaldo - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
