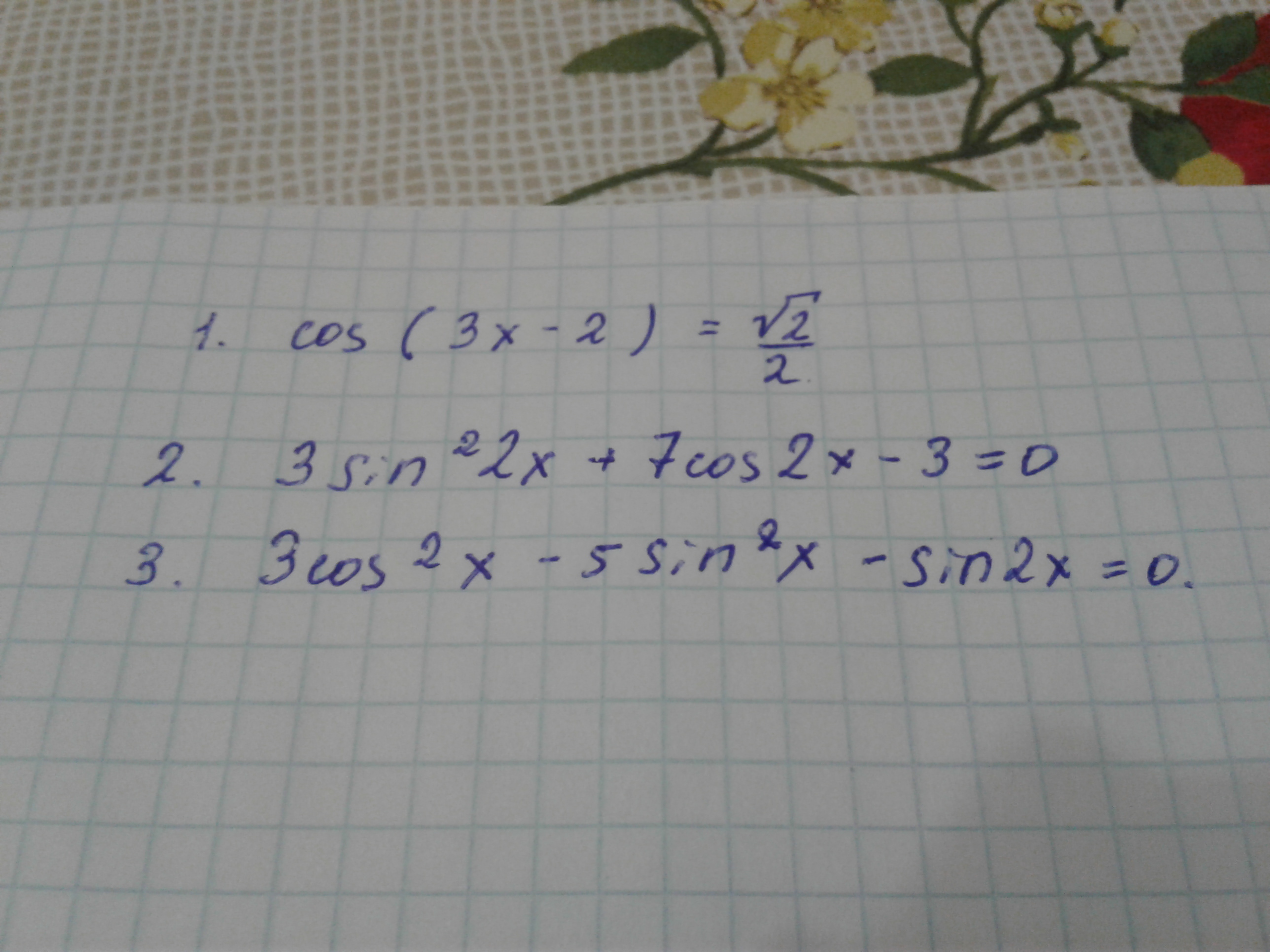Ответы 1
-
1)cos(3x-2)=√2/23x-2=±п/4+2пк,к€z3x=2±п/4+2пk,k€zx=2/3±п/12+2пk/3,k€z2)3sin²2x+7cos2x-3=03(1-cos²2x)+7cos2x-3=03-3cos²2x+7cos2x-3=0-3cos²2x+7cos2x=0cos2x(-3cos2x+7)=0cos2x=02x=п/2+пn,n€zx=п/4+пn/2,n€z-3cos2x=-7cos2x=7/3∅ x€[-1;1]3)3cos²x-5sin²x-sin2x=03cos²x-5sin²x-2sinxcosx=0 |:cos²x3-5tg²x-2tgx=0-5tg²x-2tgx+3=0tgx=t-5t²-2t+3=0D=4-4*(-5)*3=4+60=64t1=2+8/-10=-1t2=2-8/-10=-6/-10=0,6tgx=-1x=-п/4+пn,n€ztgx=0,6x=arctg0,6+пk,k€z
-
Автор:
caleshields - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Почему при объединении Испании пострадали мавры и евреи; как это повлияло на развитие страны?
-
не выполняя построения найдите координаты точек пересечения параболы y=-x2+6 и прямой y=-2x-2
-
Предмет:
Математика -
Автор:
jairo - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Выписать слова с вариантами марфем и образовать слова с чередованием: Из этих 4 строк:Чиста небесная лазурь,
Теплей и ярче солнце стало,
Пора метелей злых и бурь
Опять надолго миновала-
Предмет:
Русский язык -
Автор:
spencercooke - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Через два крана бак наполнился за 18 мини. Если бы был открыт только первый кран, то бак наполнился бы за 30 Мин. За сколько минут наполнился бы бак через один второй кран?
Спасибо-
Предмет:
Математика -
Автор:
babe - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years