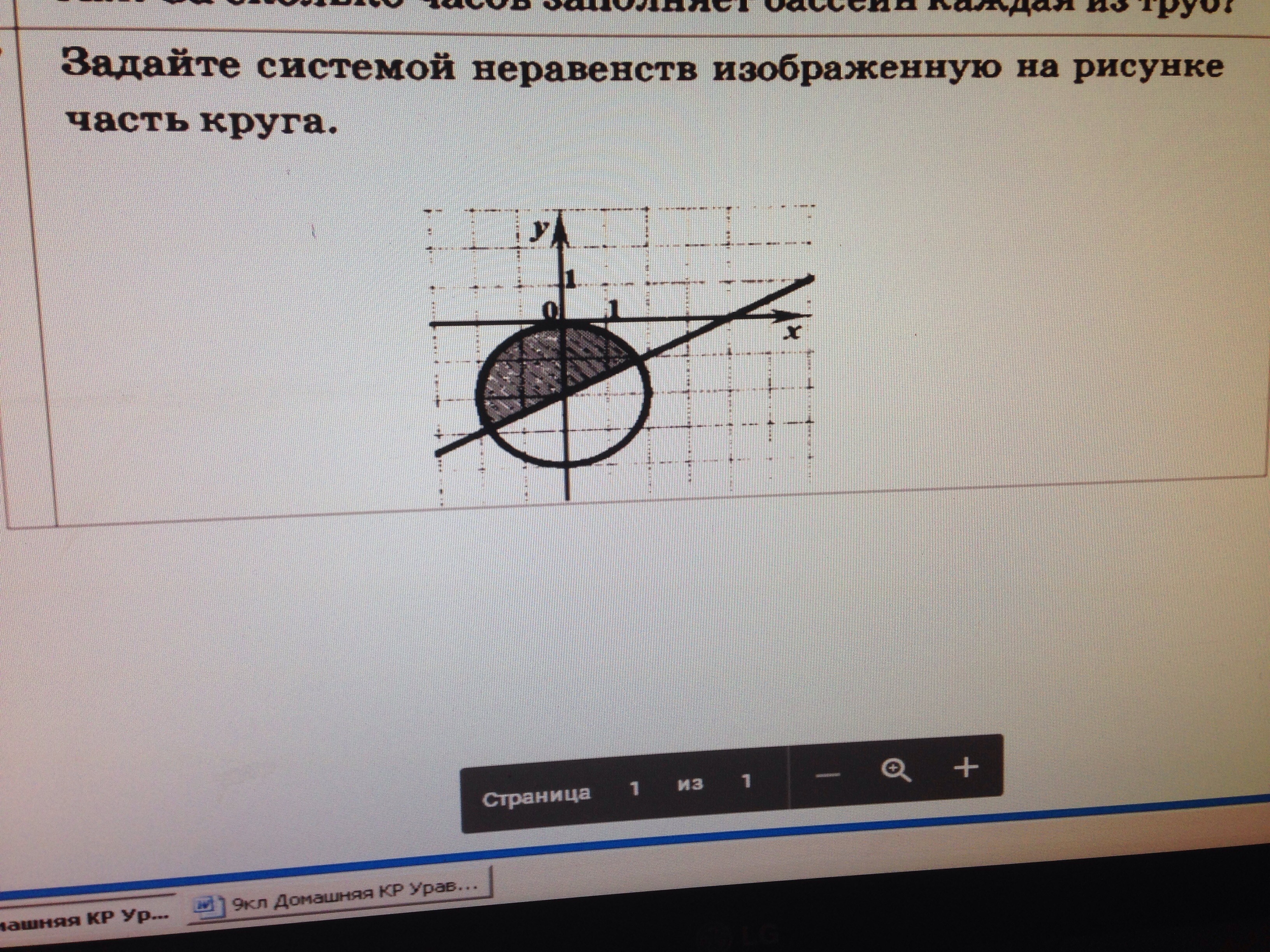
Ребят помощь очень СРОЧНО нужна!!!!!!!!!!Помогите решить задание,прошу!!!!!!!!!

круг в центре координат радиуса 2 задается формулойx²+y²=2²x²+y²=4область внутри круга, ключая сам круг будетx²+y²≤4теперь сдвинем этот руг на 2 внизx²+(y+2)²≤4 это перве неравенствотерерь зададим прямую y=kx+b, проходящую через точки (-2;-3) и (0;-2)-3=-2k+b-2=0k+bb=-2-3=-2k-2-1=-2kk=0,5прямая y=0,5x-2y≥0,5x-2  - все точки над прямой и на прямойитак получили систему неравенствx²+(y+2)²≤4y≥0,5x-2если круг и прямая не дожны входить в область, тоx²+(y+2)²<4y>0,5x-2