Задать вопрос Регистрация
Помочь другим

  • ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО С ЛОГАРИФМИЧЕСКИМ НЕРАВЕНСТВОМ!!!
    Подробное решение, буду признательна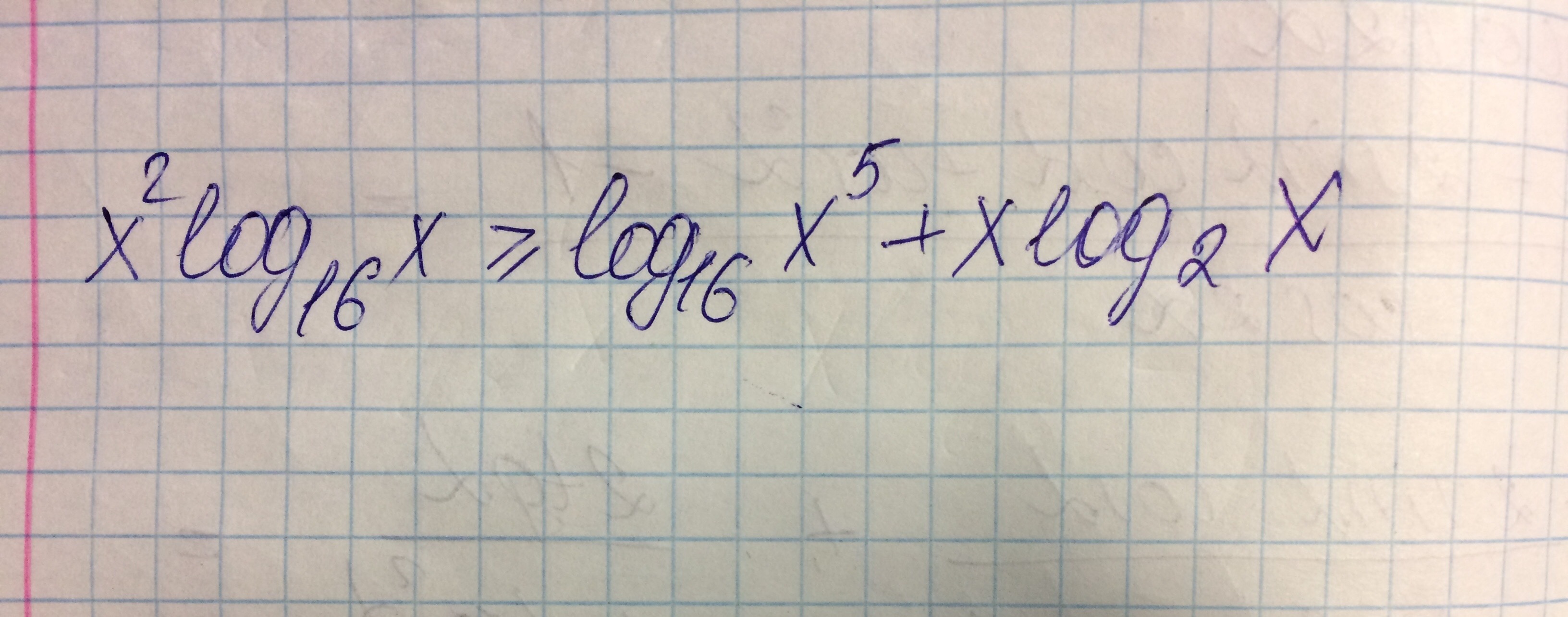

    question img

Ответы 1

  • ОДЗ х>0\displaystyle x^2log_{16}x \geq log_{16}x^5+xlog_2x x^2log_{2^4}x \geq log_{2^4}x^5+xlog_2x \displaystyle \frac{1}{4}x^2log_2x \geq \frac{5}{4}log_2x+xlog_2x |*4 \displaystyle x^2log_2x \geq 5log_2x+4xlog_2x log_2x(x^2-5-4x) \geq 0т.к. log₂x при х>0 всегда положительный то решим неравенство относительно второго множителя\displaystyle x^2-4x-5 \geq 0 \displaystyle D=16+20=36=6^2 x_1=5; x_2=-1_+_____-__________+______    -1                      5т.к. x>0 то решением будет [5;+∞)

    • Автор:

      cedricliu
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years