Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста))) решить,никак не могу понять(
    Сегодня!
    Спасибо заранее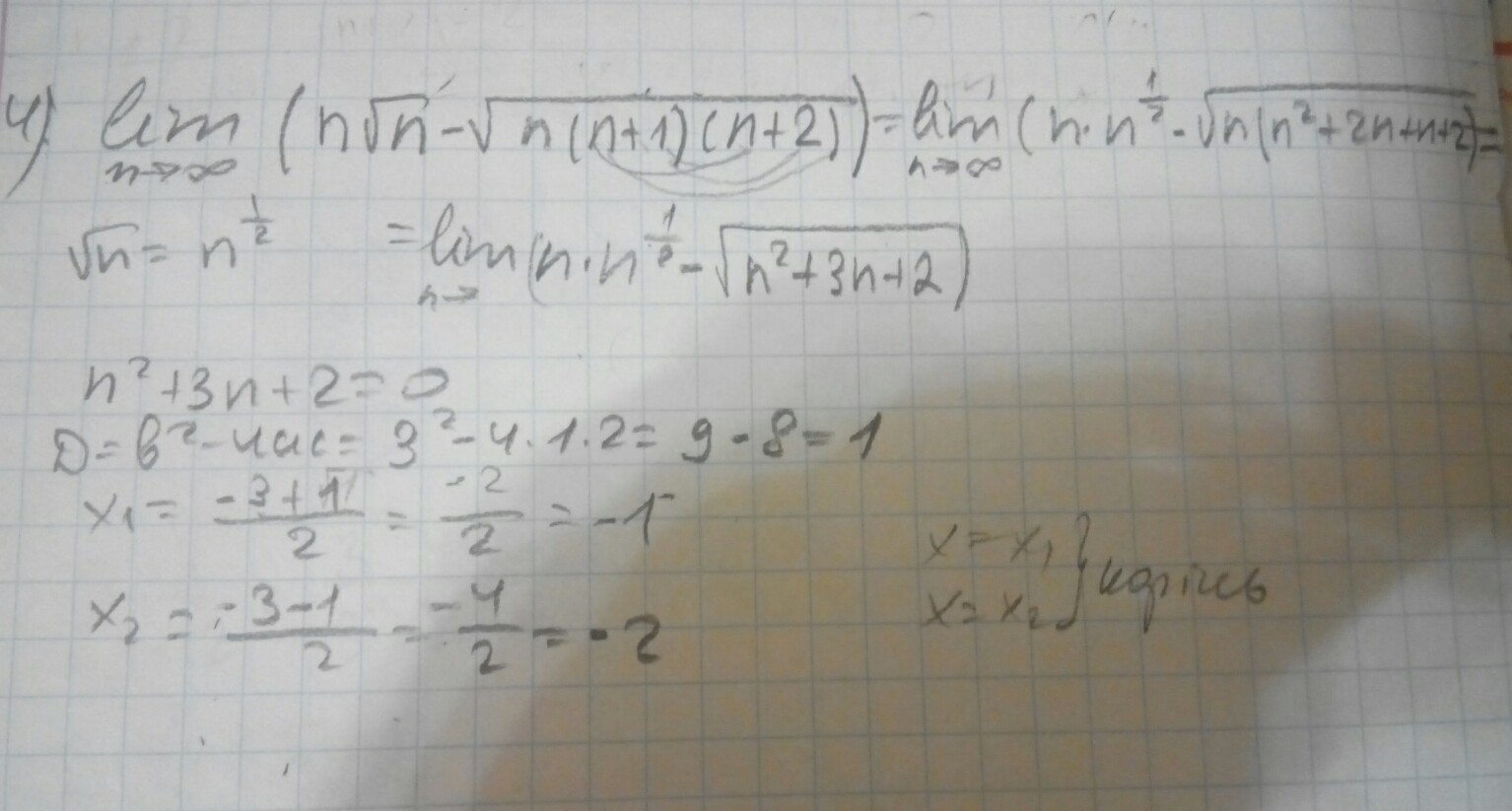

    question img

Ответы 4

  • А можете пожалуйста написать?

    • Автор:

      hays
    • 5 лет назад
    • 0
  • Здесь всё написано. Перезагрузи страницу (не с телефона), тогда всё увидишь.

    • Автор:

      jessoahl
    • 5 лет назад
    • 0
  • ок

    • Автор:

      franklin
    • 5 лет назад
    • 0
  • \lim\limits _{n \to \infty} \Big (n\sqrt{n}-\sqrt{n(n+1)(n+2)}\Big )= \lim\limits _{n \to \infty} \Big (\sqrt{n^3}-\sqrt{n^3+3n^2+2n}\Big )=\\\\= \lim\limits _{n \to \infty}\frac{(\sqrt{n^3}-\sqrt{n^3+3n^2+2n})(\sqrt{n^3}+\sqrt{n^3+3n^2+2n})}{\sqrt{n^3}+\sqrt{n^3+3n&^2+2n}}=\\\\= \lim\limits _{n \to \infty} \frac{n^3-(n^3+3n^2+2n)}{\sqrt{n^3}+\sqrt{n^3+3n^2+2n}} = \lim\limits _{n \to \infty} \frac{-3n^2-2n}{\sqrt{n^3}+\sqrt{n^3+3n^2+2n}} =[\frac{:n^2}{:n^2}]== \lim\limits _{n \to \infty} \frac{-3-\frac{2}{n}}{\sqrt{\frac{1}{n}}+\sqrt{\frac{1}{n}+\frac{3}{n^2}+\frac{2}{n^3}}} =\frac{-3-0}{0+0}=-\infty

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years